2022.05.29 2025.12.06

【scikit-learn】PCAで主成分分析をする方法

naoki-hn

Python の機械学習ライブラリである scikit-learn を使って主成分分析をする方法について解説します。また、主成分分析での次元削減についても紹介します。

1 主成分分析（PCA）
2 scikit-learn の PCA で主成分分析をする方法
3 【参考】主成分分析（PCA）における数学の理解
- 3.1 これなら分かる応用数学教室
- 3.2 プログラミングのための線形代数
4 まとめ

主成分分析（PCA）

主成分分析（PCA: Principal Component Analysis）は、元データの特徴を最もよく表す主成分と呼ばれるベクトルを計算するための解析手法です。高次元の元データを寄与率が高いいくつかの主成分へ射影することで次元削減ができるため、次元削減手法としてもよく使用されています。

主成分分析（PCA）は、Python の機械学習ライブラリである scikit-learn に実装がされており、簡単に使用することができます。

この記事では、scikit-learn の PCA を使用して主成分分析をする方法について紹介します。また、主成分分析による次元削減についても説明します。本記事では細かな数学的な説明はしません。数学的な意味合いなどを知りたい場合のために、参考書籍も紹介しますので参考にしてください。

scikit-learn の `PCA` で主成分分析をする方法

以降では、scikit-learn を使用します。インストールがされていない場合は pip でインストールをしておいてください。

pip install scikit-learn

主成分分析の使い方（`sklearn.decomposition.PCA`）

簡単な例として 2 次元のデータに対して主成分分析をする例を使って方法を説明します。データが 3 次元以上の高次元データになったとしても考え方は同じです。

scikit-learn で主成分分析を実行するには以下のようにします。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA


def main():
    """メイン関数"""

    np.random.seed(123)

    # ===== データの作成と描画
    n_point = 200
    data = np.dot(np.random.rand(2, 2), np.random.randn(2, n_point)).T
    plt.scatter(data[:, 0], data[:, 1])
    plt.axis("equal")
    plt.show()

    # ===== 主成分分析の実行
    pca = PCA(n_components=2)
    pca.fit(data)

    # 結果の表示
    print(f"主成分: \n{pca.components_}")
    print(f"分散: \n{pca.explained_variance_}")
    print(f"寄与率: \n{pca.explained_variance_ratio_}")


if __name__ == "__main__":
    main()

【実行結果】
主成分: 
[[-0.84453204 -0.53550502]
 [-0.53550502  0.84453204]]
分散: 
[0.82074725 0.11796863]
寄与率: 
[0.87432978 0.12567022]

【表示結果】

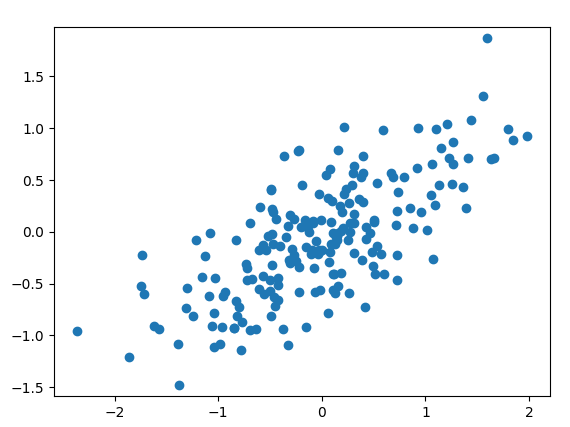
例として 2 次元正規分布を共分散行列を使って変換した入力データを使用しています。

実行結果の見方としては以下のようになります。寄与率は、主成分がどれだけデータを表現しているかを意味します。この例では、約87% は第 1 主成分でデータの特徴を表現できているということを意味しています。

内容	主成分ベクトル	主成分方向の分散	寄与率
第 1 主成分	[-0.84453204 -0.53550502]	0.82074725	0.87432978
第 2 主成分	[-0.53550502 0.84453204]	.11796863	0.12567022

以降でプログラムの細部について説明していきます。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA

主成分分析で使用する PCA は、sklearn.decomposition に含まれます。NumPy やMatplotlib はデータ操作や可視化のためのライブラリとしてインポートしています。

    np.random.seed(123)

    # ===== データの作成と描画
    n_point = 200
    data = np.dot(np.random.rand(2, 2), np.random.randn(2, n_point)).T
    plt.scatter(data[:, 0], data[:, 1])
    plt.axis("equal")
    plt.show()

この部分は PCA の対象データを用意しています。randn で標準正規分布に従う 2 次元のデータを 200 個生成し、rand で生成した $2 \times 2$ 行列で変換しています。生成したデータは、Matplotlib の scatter でデータの散布図として表示しています。

    # ===== 主成分分析の実行
    pca = PCA(n_components=2)
    pca.fit(data)

    # 結果の表示
    print(f"主成分: \n{pca.components_}")
    print(f"分散: \n{pca.explained_variance_}")
    print(f"寄与率: \n{pca.explained_variance_ratio_}")

この部分が、本題の主成分分析（PCA）を実行している部分です。PCA の引数として、n_components で主成分分析の次元を指定します。主成分分析は fit メソッドで実行します。

各計算結果は、以下を参照することで確認できます。

components_：主成分
explained_variance_：主成分方向の分散
explained_variance_ratio_：寄与率

sckit-learn は共通なインターフェースで API が作成されているため、メソッド名が分かりやすくなっています。PCA に関わらず、以下のような考え方で実装がされています。

fit()：データに対する機械学習を実行する。
transform()：データを変換する。
predict()：学習したモデルで予測を実行する。

主成分ベクトルを表示してみる

主成分分析の実行方法を見ましたが、より視覚的に主成分分析を考えてみましょう。

分析した主成分ベクトルを図上に表示してみます。また、transform を使って各主成分軸に元のデータを射影した値をグラフ化してみます。

以下のプログラムを使用します。PCA の実行部分は同じですが、主成分ベクトルを表示するための drow_vector 関数を作って矢印を描画しています。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA


def draw_vector(pt_from, pt_to, ax=None):
    """ベクトル描画関数

    Args:
        pt_from: 矢印の始点座標
        pt_to: 矢印の終点座標
        ax: 描画対象axis (デフォルト:None)
    """

    if ax is None:
        ax = plt.gca()
    arrowprops = dict(arrowstyle="->", linewidth=2, shrinkA=0, shrinkB=0)
    ax.annotate("", pt_to, pt_from, arrowprops=arrowprops)


def main():
    """メイン関数"""

    np.random.seed(123)

    # ===== データの作成と描画
    n_point = 200
    data = np.dot(np.random.rand(2, 2), np.random.randn(2, n_point)).T
    plt.scatter(data[:, 0], data[:, 1])
    plt.axis("equal")

    # ===== 主成分分析の実行
    pca = PCA(n_components=2)
    pca.fit(data)

    # 結果の表示
    print(f"主成分: \n{pca.components_}")
    print(f"分散: \n{pca.explained_variance_}")
    print(f"寄与率: \n{pca.explained_variance_ratio_}")

    # ===== 主成分ベクトルを表示してみる
    for var, vector in zip(pca.explained_variance_, pca.components_):
        # 標準偏差分の長さのベクトルを作成
        vec = vector * np.sqrt(var)
        draw_vector(pca.mean_, pca.mean_ + vec)
    plt.show()

    # =====
    data_pca = pca.transform(data)
    plt.scatter(data_pca[:, 0], data_pca[:, 1])
    plt.axis("equal")
    plt.xlabel("component1")
    plt.ylabel("component2")
    plt.show()


if __name__ == "__main__":
    main()

【実行結果】
主成分: 
[[-0.84453204 -0.53550502]
 [-0.53550502  0.84453204]]
分散: 
[0.82074725 0.11796863]
寄与率: 
[0.87432978 0.12567022]

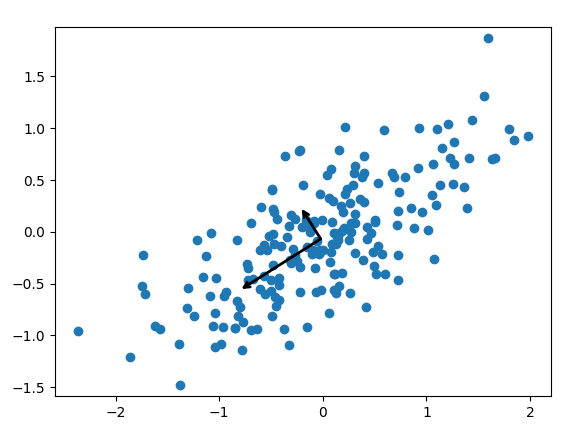
【主成分ベクトルの表示】

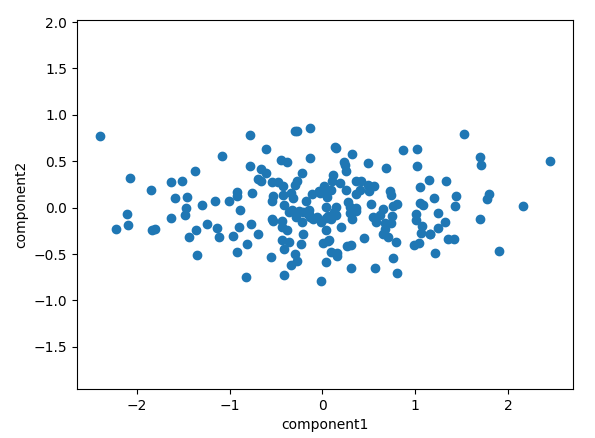
【主成分ベクトル軸へ変換した後のプロット】transform 後

まず、主成分ベクトルの表示について見てみましょう。結果を見ると各主成分の矢印がデータの広がり方向を表したベクトルになっていることが分かります。このように、主成分分析はデータの特徴を表す方向を計算しています。

次に、各軸への変換した結果を見てみます。

    data_pca = pca.transform(data)

transform メソッドでは、各主成分軸へ元のデータを射影した時の各軸の値を計算できます。このように元データを主成分軸へ変換することが可能です。

主成分分析による次元削減

主成分分析の主な使用方法の 1 つに次元削減があります。多くの場合、高次元のデータは寄与率の高い主成分だけで十分に説明できることが多いです。寄与率が低い主成分はただの雑音（ノイズ）であることが多いため、適切な次元に落とすことでノイズを除去することができる場合もあります。

どの程度の次元まで削減するかは、寄与率の大きい方から足していった累積寄与率が XX % 以上になるまでといったような方法が使われます。

高次元では分かりにくいので、今回は 2 次元から 1 次元に次元削減する例で見てみます。n > mとしたときに、n 次元から m 次元に次元削減するような場合も考え方は同じになります。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA


def main():
    """メイン関数"""

    np.random.seed(123)

    # ===== データの作成と描画
    n_point = 200
    data = np.dot(np.random.rand(2, 2), np.random.randn(2, n_point)).T
    plt.scatter(data[:, 0], data[:, 1])

    # ===== 主成分分析の実行(1次元)
    pca = PCA(n_components=1)
    pca.fit(data)

    # 結果の表示
    print(f"主成分: \n{pca.components_}")
    print(f"分散: \n{pca.explained_variance_}")
    print(f"寄与率: \n{pca.explained_variance_ratio_}")

    # ===== 一次元へ変換
    data_pca = pca.transform(data)
    # 2次元空間へ戻してみて確認してみる
    data_new = pca.inverse_transform(data_pca)
    plt.scatter(data_new[:, 0], data_new[:, 1])

    plt.axis("equal")
    plt.show()


if __name__ == "__main__":
    main()

【実行結果】
主成分: 
[[-0.84453204 -0.53550502]]
分散: 
[0.82074725]
寄与率: 
[0.87432978]

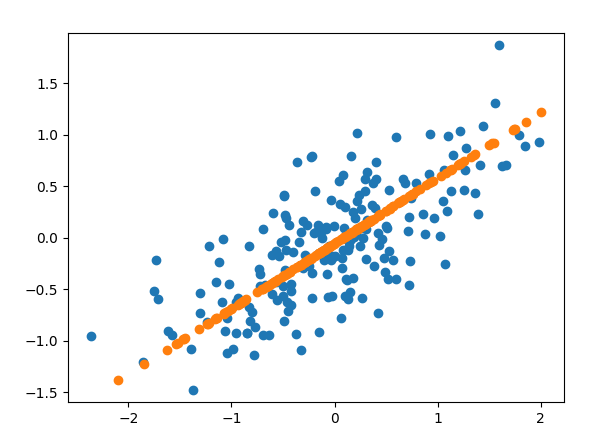
【表示結果】

PCA の実行部分は、ほとんど同じですが、n_components=1 で 1 次元に変換するようにしています。

    # ===== 一次元へ変換
    data_pca = pca.transform(data)
    # 2次元空間へ戻してみて確認してみる
    data_new = pca.inverse_transform(data_pca)
    plt.scatter(data_new[:, 0], data_new[:, 1])

上記の部分で 1 次元データへ変換（主成分ベクトルへの射影）を行っています。

この時点での data_pca は、主成分方向のベクトルの値に変換されているのですが、PCA には、inverse_transform メソッドがあり元の軸の値に戻すことができます。元の軸に戻した値が、data_new でプロットしたものが図のオレンジの点です。

この結果を見ると、主成分方向の軸にデータが射影されていることがよく分かります。

このように、主成分分析での次元削減とは、主成分の軸に射影をして次元を落としていることを意味しています。例えば、3 次元のデータを 2 次元に削減する場合は、元の 3 次元データは主成分で表される 2 次元の平面へ直角に射影されます。

より高次元となると視覚的に見ることはできませんが、上記と同様のことが高次元空間で起こっています。