ニューラルネットワークの活性化関数まとめ (sigmoid, ReLU, Leaky ReLU, swish, h-swish, softmax)

ニューラルネットワークを学習すると必ず勉強することになる活性化関数について、NumPyを用いた実装を含めて紹介します。具体的に活性化関数としては、シグモイド（sigmoid）, ReLU, Leaky ReLU, swish, h-swish, softmaxといった関数を紹介します。

活性化関数とは

活性化関数とは、ニューラルネットワークの各層の出力前に適用する関数の事を言います。ニューラルネットワークでは、ニューロンをネットワーク上につなげたようなモデルを作り、それぞれの重みを学習させます。ニューラルネットワークを構成するニューロンの構成概要は以下のようにな図示できます。

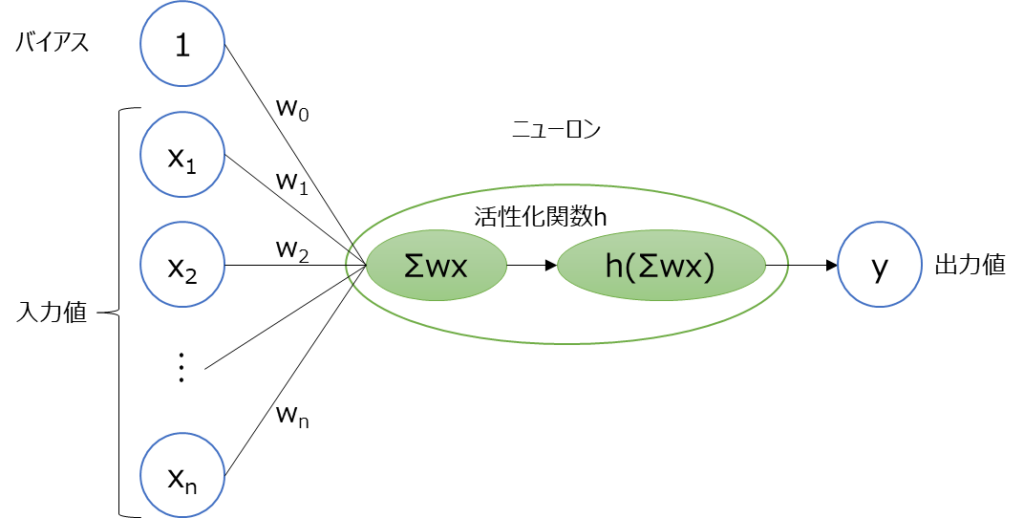
左側の$x_{1}$~$x_{n}$は入力値です。その他にバイアスとして1があります。$w_{0}$~$w_{n}$は重みパラメーターと言い学習するパラメータになります。具体的にはニューロンでは以下のような計算がされます。

\[
\boldsymbol{x}=
\left[
\begin{array}{r}
1\\
x_{1}\\
x_{2}\\
…\\
x_{n}
\end{array}
\right],
\quad
\boldsymbol{w}=
\left[
\begin{array}{r}
w_{0}\\
w_{1}\\
w_{2}\\
…\\
w_{n}
\end{array}
\right]
\]

\[\sum wx = \boldsymbol{w^{\top}x} = w_{0} + w_{1}x_{1} + w_{2}x_{2} + … + w_{n}x_{n}\]

\[y = h(\sum wx)\]

今回の主役となる活性化関数は上記における関数$h$です。

$\sum wx$は、線形変換しているわけですが、活性化関数$h$を用いることで非線形性をモデルに持たせることができるようになります。非線形性をモデルが持たない場合、例えば分類問題では、線形（直線で）分離できる問題しか解けなくなります。

活性化関数にはたくさんの種類があり、問題に応じて適切なものを選ぶようにする必要があります。本記事では、色々な活性化関数の式や形状を紹介するとともに、NumPyでの実装例を含めて紹介していきたいと思います。

色々な活性化関数とNumPyによる実装方法

以降では、活性化関数の具体的な式を示すとともに、NumPyによる実装方法を紹介していきます。

シグモイド（sigmoid）関数

シグモイド（sigmoid）関数は、ニューラルネットワークで古くからよく使用されている活性化関数です。シグモイド（sigmoid）関数は以下のような式となっています。

\[
h_{sigmoid}(x) = \frac{1}{1+e^{-x}}
\]

NumPyでのシグモイド（sigmoid）関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def sigmoid(x):
    """シグモイド関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return 1 / (1 + np.exp(-x))


def main():
    """メイン関数"""
    
    x = np.arange(-10, 10, 0.1)
    y = sigmoid(x)

    # グラフの描画
    plt.plot(x, y, label="sigmoid(x)")
    plt.title("sigmoid function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()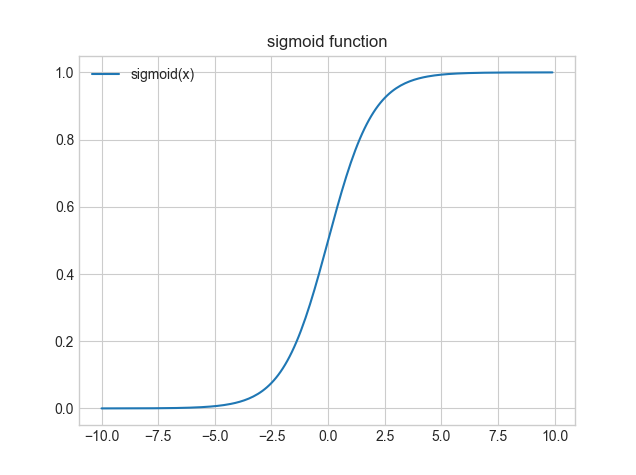

シグモイド（sigmoid）関数は、0~1の間の出力を取ることが特徴です。例えば2値分類のような問題では、0か1かに分類するようなことを考えるできるわけですが、シグモイド関数を用いるとAの確率が0.8、Bの確率は0.2のように捉えることができます。このようにシグモイド曲線の値は確率として使用できます。

ReLU関数

ReLU（Rectified Linear Unit）関数も非常によく使われる活性化関数です。シグモイド関数がニューラルネットワークの歴史の中では古くから利用されてきたのですが、最近のディープニューラルネットワークにおける中間層の活性化関数としては、ReLU関数が主に用いられることが多いです。

ReLU関数は以下のような式となっています。

\[
\begin{eqnarray}
h_{relu}(x)
=
\begin{cases}
0 & ( x \lt 0 ) \\
x & ( x \geq 0 )
\end{cases}
\end{eqnarray}
\]

NumPyでのReLU関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def relu(x):
    """ReLU関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return np.maximum(0, x)


def main():
    """メイン関数"""

    x = np.arange(-10, 10, 0.1)
    y = relu(x)

    # グラフの描画
    plt.plot(x, y, label="relu(x)")
    plt.title("relu function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()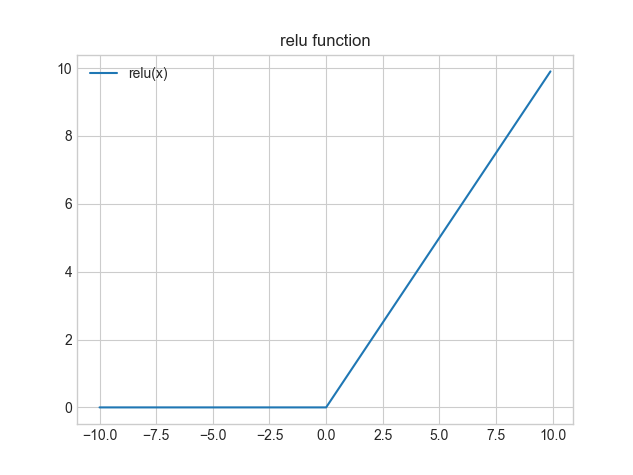

ReLU関数では、入力値が0未満であれば0を、0以上であれば入力値をそのまま出力とします。

Leaky ReLU関数

ReLUの欠点の一つとして、入力値が0未満（$x \lt 0$）の範囲では0で一様の出力をしてしまうということがあります。ニューラルネットワークでは、目的関数の勾配からパラメータの最適化をするわけですが、この範囲の勾配（微分値）は0であるので勾配がなくなってしまい学習がしにくくなる場合があります。そこで、勾配がなくならないように工夫した関数がLeaky ReLU関数です。

Leaky ReLU関数は以下のような式となっています。

\[
h_{leakyrelu}(x) = max(\alpha x, x)
\]

NumPyでのLeaky ReLU関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def leaky_relu(x, alpha=0.1):
    """Leaky ReLU関数

    Args:
        x: 入力
        alpha: α値(デフォルト: 0.1)

    Returns:
        出力
    """
    return np.where(x >= 0, x, alpha * x)


def main():
    """メイン関数"""

    x = np.arange(-10, 10, 0.1)
    y = leaky_relu(x)

    # グラフの描画
    plt.plot(x, y, label="leaky_relu(x)")
    plt.title("leaky relu function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()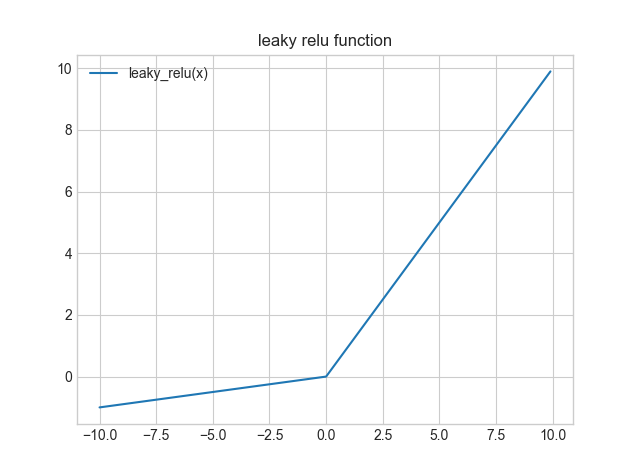

Leaky ReLU関数では、$x \lt 0$の時には$\alpha$をかけた値を出力をします。$\alpha$は、0.1や0.01のように小さな値を使います。

ReLU6関数

ReLU関数には他にも派生形があります。

スマートフォンなどのエッジデバイスでのディープラーニングの利用では、より軽量な計算量で処理ができるようにする必要があります。画像認識における軽量なモデルにMobileNetというものがありますが、MobileNet V2で使用された活性化関数としてReLU6関数というものがあります。※MobileNetはV1, V2, V3と改善がされています。

ReLU6関数は以下のような式となっています。

\[
h_{relu6}(x) = min(max(0, x), 6)
\]

NumPyでのReLU6関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def relu6(x):
    """ReLU6関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return np.minimum(np.maximum(0, x), 6)


def main():
    """メイン関数"""

    x = np.arange(-10, 10, 0.1)
    y = relu6(x)

    # グラフの描画
    plt.plot(x, y, label="relu6(x)")
    plt.title("relu6 function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()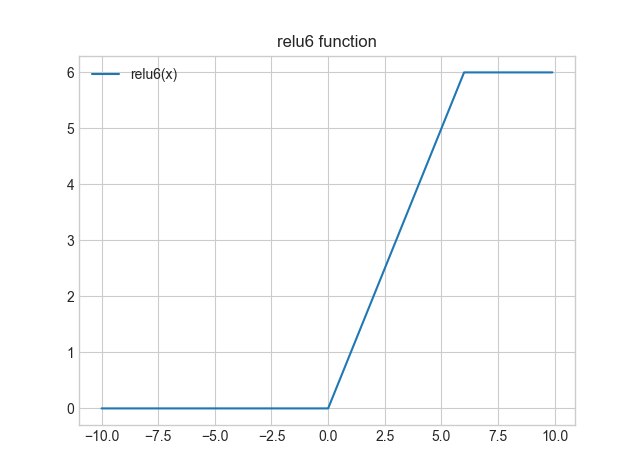

ReLU6関数は、ReLU関数の出力を6で頭打ちにしてしまった関数となっています。ReLUは入力が大きくなるとそのまま大きな値が活性化関数の出力として出力されますが、大きすぎる値は制度に悪影響を与えるという考えがもとになっています。

swish関数

swish（スウィッシュ）関数は、ReLUに比べて高い性能を示すとして2017年にGoogleの研究グループから発表された活性化関数です。シグモイド関数を使用した関数を使用しているものとなっていて、SiLU（Sigmoid-weighted Linear Unit）関数とも言われるようです。

ReLU6関数は以下のような式となっています。$\sigma(x)$はシグモイド関数だと理解ください。

\[
h_{swish}(x) = x\cdot\sigma(x)
\]

NumPyでのswish関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def sigmoid(x):
    """シグモイド関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return 1 / (1 + np.exp(-x))


def swish(x):
    """swish関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return x * sigmoid(x)


def main():
    """メイン関数"""

    x = np.arange(-10, 10, 0.1)
    y = swish(x)

    # グラフの描画
    plt.plot(x, y, label="swish(x)")
    plt.title("swish function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()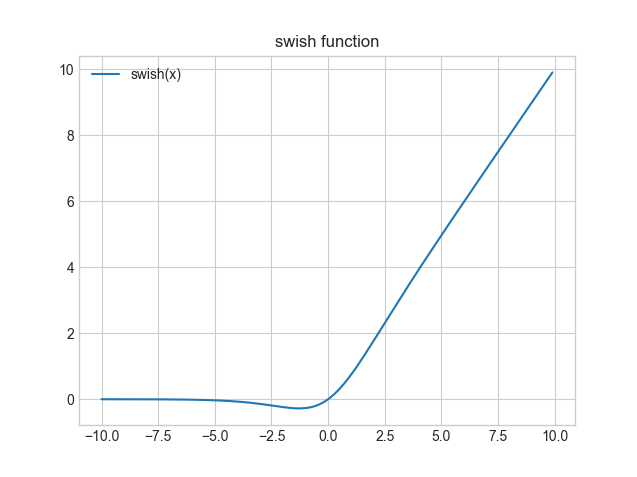

swish関数では、ReLU関数に非常に似ている曲線であることが分かるかと思います。$(0, 0)$付近を見てもらうと分かりますが少し下に膨らんだような滑らかな曲線になっていることが分かります。また、$x$が大きくなっていくとシグモイド関数は1に近づいていくので、ほぼ$x$と同じになります。

現在のディープニューラルネットワークで中間層の活性化関数としてはReLUを採用するのが一般的となっていますが、swishはReLU以外の関数として比較的有名な関数の一つと言われています。

h-swish関数

ReLU6関数のところでも少し説明しましたが、エッジデバイスでの画像認識における軽量なモデルであるMobileNetのV3では、一部の活性化関数を上記のswish関数をもとにしたh-swish関数が使用されています。

h-swish関数は以下のような式となっています。swishのシグモイド関数をReLU6関数に置き換えたような形をしています。ここで$ReLU6(x)$の部分がReLU6関数だと理解ください。

\[
h_{hswish}(x) = x\cdot\frac{ReLU6(x + 3)}{6}
\]

NumPyでのh-swish関数の実装とグラフ描画例は以下になります。

import matplotlib.pyplot as plt
import numpy as np

plt.style.use("seaborn-whitegrid")


def relu6(x):
    """ReLU6関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return np.minimum(np.maximum(0, x), 6)


def h_swish(x):
    """h-swish関数

    Args:
        x: 入力

    Returns:
        出力
    """
    return x * relu6(x + 3) / 6


def main():
    """メイン関数"""
    
    x = np.arange(-10, 10, 0.1)
    y = h_swish(x)

    # グラフの描画
    plt.plot(x, y, label="h_swish(x)")
    plt.title("h-swish function")
    plt.legend()
    plt.show()


if __name__ == "__main__":
    main()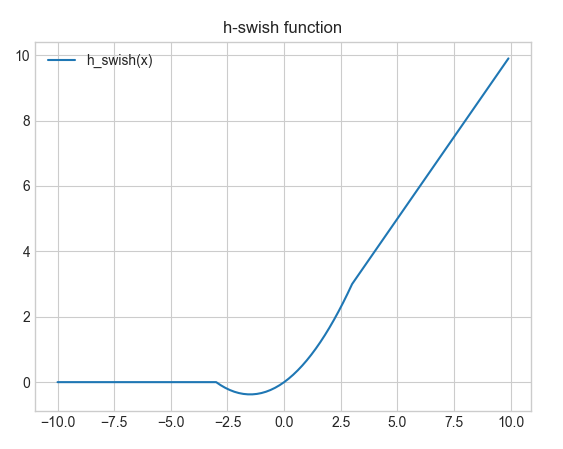

softmax関数

ニューラルネットワークにおける多クラス分類問題で出力層でよく用いられる活性化関数としてsoftmax関数があります。

ソフトマックス関数を図で書いてみると以下のような形となります。すべての線がつながっているのは、出力が全ての入力信号から影響を受けるという意味です。例えば、分類問題に当てはめると$y_{1}$が犬、$y_{2}$が猫である確率値を表すみたいな感じになると思ってください。

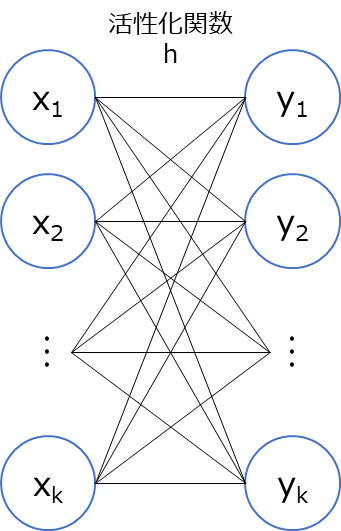
softmax関数は以下のような式となっています。

\[
y_{i} = \frac{exp(x_{i})}{\sum_{j=1}^{k}exp(x_{j})}
\]

NumPyでのsoftmax関数の実装例は以下になります。まずは、シンプルに上記式を実装してみます。後述しますが以下のプログラムには実装上の問題があるのですが、まずは実装してみましょう。

import numpy as np


def softmax(x):
    """softmax関数

    Args:
        x: 入力

    Returns:
        出力
    """
    exp_x = np.exp(x)
    sum_exp = np.sum(exp_x)
    return exp_x / sum_exp


def main():
    """メイン関数"""
    
    x = np.array([0.5, 2.8, 5.0, 1.0, 3.0])
    y = softmax(x)

    print(f"softmax(x): {y}")
    print(f"sum(softmax(x))): {np.sum(y)}")


if __name__ == "__main__":
    main()

【実行結果】
softmax(x): [0.00870909 0.08686608 0.7839675  0.01435887 0.10609846]
sum(softmax(x))): 1.0

softmax関数の特徴は、出力値が0~1の間になることです。シグモイド関数に似ていますね。また、上記例でも出力値を合計した結果を示していますが、出力の合計は1になります。

この特徴は確率の観点で非常に重要な意味を持っています。例えば3クラス分類問題を考えた場合に、$y_{1}=0.05$、$y_{2}=0.8$、$y_{3}=0.15$になったとしましょう。この時には2番目のクラスである確率が最も高い予測結果であると判断できます。また、次に近いクラスとしては3番目で、1番目のクラスである確率は最も低いことも予想できます。このようにsoftmax関数では確率的な理解をできる点で、分類問題の出力層ではよく使用されます。

softmax関数実装上の注意

さて、上記でsoftmax関数を実装したのですが、実は実装上に問題があります。main関数部分を以下のようにして実行してみてください。

def main():
    """メイン関数"""

    x = np.array([1010, 1020, 1000, 990, 1050])
    y = softmax(x)

    print(f"softmax(x): {y}")
    print(f"sum(softmax(x))): {np.sum(y)}")

【実行結果】
RuntimeWarning: overflow encountered in exp
  exp_x = np.exp(x)
RuntimeWarning: invalid value encountered in true_divide
  return exp_x / sum_exp
softmax(x): [nan nan nan nan nan]
sum(softmax(x))): nan

結果を見てみると、nanになってしまっていることが分かります。これは、オーバーフローを起こしてしまっていることが原因です。例えば、$exp(1000)$では計算結果として無限大を表すinfが返ってきます。

このオーバーフローに対応するために、以下のような式変形の特徴を利用して改善する方法があります。

\[
\begin{eqnarray}
y_{i} = \frac{exp(x_{i})}{\sum_{j=1}^{k}exp(x_{j})}
&=& \frac{C\cdot exp(x_{i})}{C\cdot\sum_{j=1}^{k}exp(x_{j})} \\
&=&\frac{exp(x_{i} + logC)}{\sum_{j=1}^{k}exp(x_{j} + logC)} \\
&=&\frac{exp(x_{i} + C^{\prime})}{\sum_{j=1}^{k}exp(x_{j} + C^{\prime})}
\end{eqnarray}
\]

分母と分子に$C$という任意の定数をかけています。両方にかけているので元々の式と全く同じです。そこから、定数を指数関数の中に入れて定数部分を最終的に$C^{\prime}$としています。

これは、入力値に任意の定数を足し算、または引き算しても結果は変わらないということを意味します。オーバーフロー対策としては一般的には入力信号の最大値を引きます。

では対策をしたsoftmax関数で先ほどオーバーフローした例を実行してみます。

import numpy as np


def softmax(x):
    """softmax関数(オーバーフロー対策版)

    Args:
        x: 入力

    Returns:
        出力
    """
    c = np.max(x)
    # オーバーフロー対策
    exp_x = np.exp(x - c)
    sum_exp = np.sum(exp_x)

    return exp_x / sum_exp


def main():
    """メイン関数"""

    x = np.array([1010, 1020, 1000, 990, 1050])
    y = softmax(x)

    print(f"softmax(x): {y}")
    print(f"sum(softmax(x))): {np.sum(y)}")


if __name__ == "__main__":
    main()

【実行結果】
softmax(x): [4.24835426e-18 9.35762297e-14 1.92874985e-22 8.75651076e-27
 1.00000000e+00]
sum(softmax(x))): 1.0

先ほどはnanとなってしまっていたところが計算できていることが分かるかと思います。

まとめ

本記事では、ニューラルネットワークでとても重要な要素となる活性化関数について色々と紹介するとともに、NumPyでの実装例を紹介しました。

活性化関数の選択にはある程度のルールのようなものがあります。例えば中間層の活性化関数としてはReLU関数が一般的とか、出力層では二値分類だとsigmoid関数、多クラス分類だとsoftmax関数だとかいった感じです。

ただ、ニューラルネットワークの世界では、必ずこの活性化関数が精度がよくなるということはありません。色々な種類がある事を学んで、色々と試せるようにすることが大事なのかなと思っています。

【Python Tech】Pythonプログラミングガイド本サイトで紹介しているPython入門、応用に関する記事のまとめページです。Python文法の入門から高度な内容、おすすめの書籍についても紹介しています。また、機械学習等のデータ分析やGUI開発、近年話題の生成AI等のトピックスについても含んでいます。...