【scikit-learn】KernelPCAでカーネル主成分分析をする方法

Python の機械学習ライブラリである scikit-learn の KernelPCA を使って カーネル主成分分析をする方法について解説します。カーネル主成分分析をして変換をすることで線形分離不可能なデータが非線形分離ができることを見ていきたいと思います。
目次
カーネル主成分分析
主成分分析(Principal Component Analysis: PCA)は、元データの特徴を最もよく表す主成分のベクトルを計算するための解析手法です。PCAでは、高次元のデータを寄与率が高いいくつかの主成分へ射影することで次元削減できました。
今回紹介する「カーネルPCA(KernelPCA)」はデータが線形分離不可能なデータに適用し、変換をかけることで線形分離できるようなデータに変換することができます。線形分離できるようなデータに変換できれば、線形の分類器を使って容易にデータを分類できるようになります。
カーネルPCA(KernelPCA)は、Python の機械学習ライブラリである scikit-learnに実装されています。この記事では、scikit-learn の KernelPCA を使って線形分離できないデータを変換してみたいと思います。
scikit-learn の KernelPCAでカーネル主成分分析をする方法
KernelPCA の利用には scikit-learn のインストールが必要です。インストールされていない場合は、pip によりインストールしておいてください。
pip install scikit-learn
カーネルPCAの使い方
(sklearn.decomposition.KernelPCA)
実装例(circles データ)
scikit-learn のデータに用意されている make_circles を使って生成したデータで、線形分離不可能なデータを線形分離できるように変換してみます。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from sklearn.decomposition import KernelPCA
def main():
"""メイン関数"""
np.random.seed(0)
# ===== データの用意・表示
data, label = make_circles(n_samples=1000, noise=0.1, factor=0.2)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="x")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")
plt.title("circle data")
# ===== カーネルPCAのモデル生成・学習
k_pca = KernelPCA(n_components=2, kernel="rbf", gamma=15)
k_pca.fit(data, label)
# ===== 主成分軸への変換
trans_data = k_pca.transform(data)
# ===== 変換結果を表示
plt.figure()
plt.scatter(trans_data[label == 0, 0], trans_data[label == 0, 1], marker="x")
plt.scatter(trans_data[label == 1, 0], trans_data[label == 1, 1], marker="^")
plt.title("kernel pca")
plt.show()
if __name__ == "__main__":
main()【実行結果】
以降でプログラムの各部分について内容を説明します。
データの用意
np.random.seed(0)
# ===== データの用意・表示
data, label = make_circles(n_samples=1000, noise=0.1, factor=0.2)
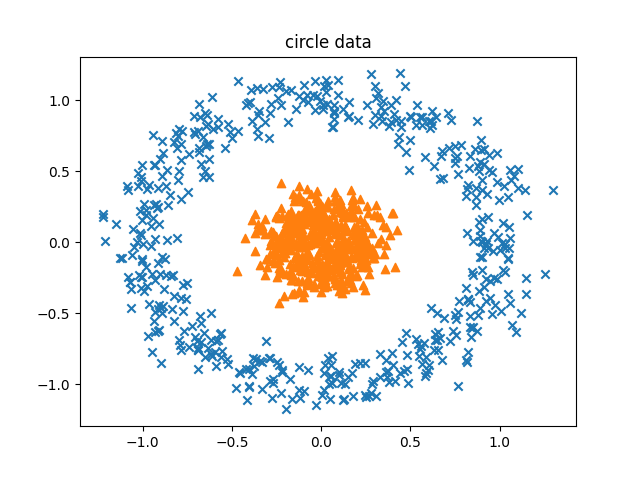
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="x")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")
plt.title("circle data")対象となるデータを生成して描画しています。描画結果を見て分かる通り、内側の円と外側の円で分かれているデータとなっています。このデータを線形分離(直線で分離)することは困難であることが分かると思います。
カーネルPCAの実行と変換
# ===== カーネルPCAのモデル生成・学習
k_pca = KernelPCA(n_components=2, kernel="rbf", gamma=15)
k_pca.fit(data, label)
# ===== 主成分軸への変換
trans_data = k_pca.transform(data)カーネルPCAのモデルを生成して学習している部分です。KernelPCA のハイパーパラメータとしては以下のようなものを設定しています。
n_components:主成分の数を指定します。kernel:カーネル関数を指定します。デフォルトは"linear"(線形)ですが、今回は"rbf"(動径基底関数)を指定しています。gamma:rbfのパラメータを指定します。
モデルの学習は fit メソッドを使用し、主成分軸への変換は transform メソッドで変換します。
変換結果の表示
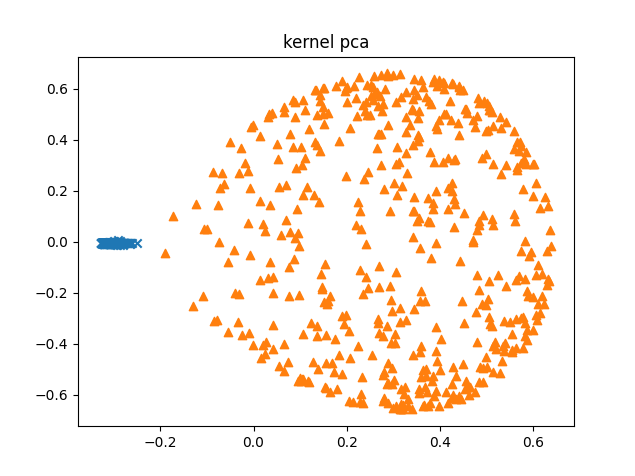
# ===== 変換結果を表示
plt.figure()
plt.scatter(trans_data[label == 0, 0], trans_data[label == 0, 1], marker="x")
plt.scatter(trans_data[label == 1, 0], trans_data[label == 1, 1], marker="^")
plt.title("kernel pca")
plt.show()最後に上記の部分では transform メソッドで変換したデータを表示しています。
元データに対して学習したモデルで変換 (transform) をかけると、結果を見てもわかるようにもともと線形分離不可能であったデータが左右の二つのデータの集まりに分離されて、線形分離可能なようになっていることが分かります。
このように KernelPCA を使った分析・変換により線形分離不可能であったデータを線形分離可能な形に変換することが可能です。
ただし、KernelPCA でデータに対して変換をかけたとしても必ず線形分離できる形に変換されるとは限りません。元データの特徴や、ハイパーパラメータの指定によっても変換の形は変わるためです。対象としているデータに対してハイパーパラメータを変えて色々と試してみると面白いかと思います。
実装例(moonsデータ)
scikit-learn のデータセットに make_moons というものもあるので同じように適用してみます。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons
from sklearn.decomposition import KernelPCA
def main():
"""メイン関数"""
np.random.seed(0)
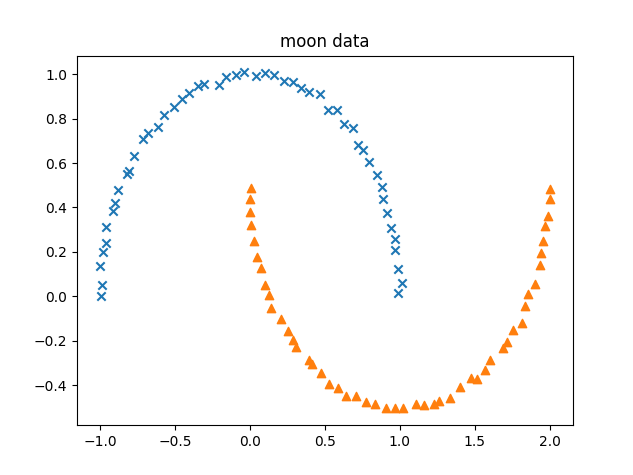
# ===== データの用意・表示
data, label = make_moons(n_samples=100, noise=0.01)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="x")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")
plt.title("moon data")
# ===== カーネルPCAのモデル生成・学習
k_pca = KernelPCA(n_components=2, kernel="rbf", gamma=15)
k_pca.fit(data, label)
# ===== 主成分軸への変換
trans_data = k_pca.transform(data)
# ===== 変換結果を表示
plt.figure()
plt.scatter(trans_data[label == 0, 0], trans_data[label == 0, 1], marker="x")
plt.scatter(trans_data[label == 1, 0], trans_data[label == 1, 1], marker="^")
plt.title("kernel pca")
plt.show()
if __name__ == "__main__":
main()【実行結果】
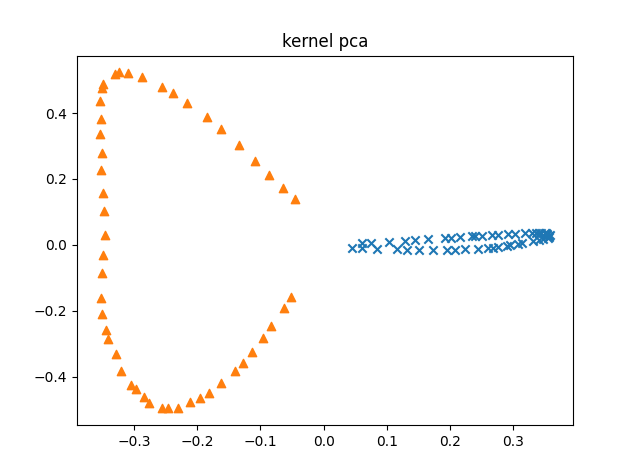
コードの構成は circles データに適用した場合と同様なので説明は省略します。
結果を見てみると月形のデータで線形分離不可能なデータが線形分離可能な形になっているのが分かります。形状が面白い例ですので紹介しました。
まとめ
Python の機械学習ライブラリである scikit-learn の KernelPCA を使ってカーネル主成分分析をする方法について紹介しました。
カーネル主成分分析をすることで、線形分離不可能なデータが線形分離できるようになることが分かりました。ただし、元データの特徴やパラメータの設定により必ずしも線形分離可能なデータに変換できるわけではないことは注意しましょう。
上記で紹介しているソースコードについては Github にて公開しています。参考にしていただければと思います。



の使用方法.jpg)



