Pythonの機械学習ライブラリであるscikit-learnを使ってサポートベクターマシン(SVM)を使用する方法について解説します。
Contents
サポートベクターマシン(SVM)
サポートベクターマシン(SVM)は、教師ありの機械学習で用いるパターン認識のモデルの一つです。サポートベクターマシンは、分類問題や回帰問題へ適用できるモデルとなっています。
サポートベクターマシンの理解で重要になってくるのが「サポートベクター」と「マージンの最大化」です。以下の画像でイメージしてみましょう。
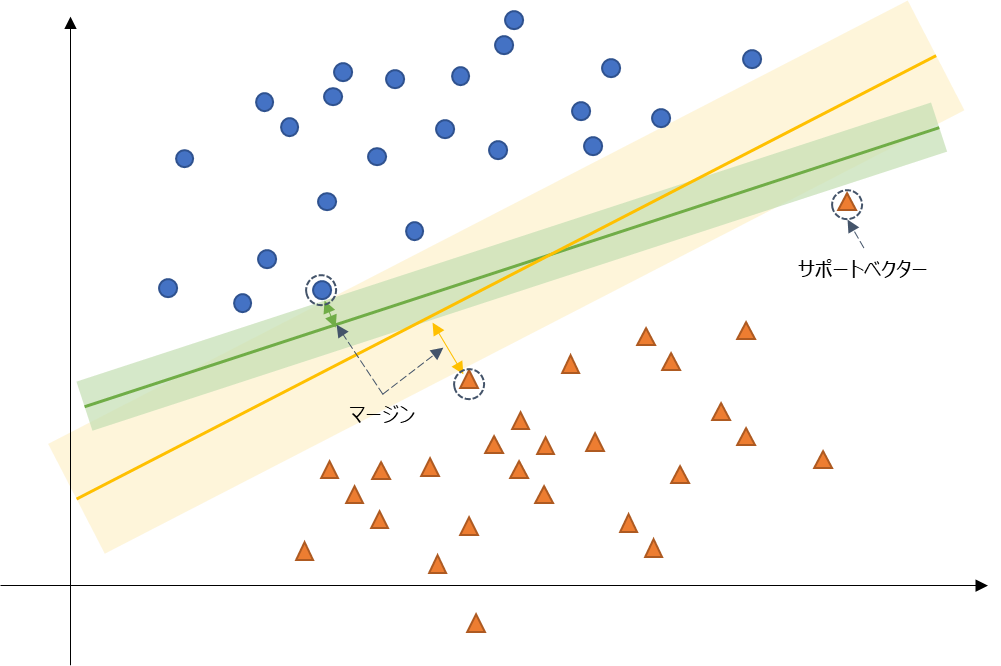
上記は、〇と△のデータを線形に分類する場合を例にしたものです。この時、二つのデータを分類するような直線は緑線や黄線のようにいくつも引けるかと思います。直線に並行するような領域(薄い色の範囲)を広げていくと、各データに接するようなデータ(点線で丸で囲んだ点)があります。このようなデータを「サポートベクター」と言います。そして、線からサポートベクターまでの距離(幅)を「マージン」と言います。
サポートベクターマシンは、このマージンを最大化するようなモデルが最適なモデルとして選択されます。上記は簡単な線形での分類の例ですが、サポートベクターマシンではカーネル法と組み合わせることで非線形な分類や回帰にも適用できます。
また、上記のようにきれいに分類できる例ではいいですが、境界線があいまいなデータが世の中にはたくさん存在します。このような場合には、ソフトマージンと言って、多少のデータはマージンの中に入っても構わないとするような方法があります。
この記事では、Pythonの機械学習ライブラリであるscikit-learnを用いてサポートベクターマシン(SVM)を使ったデータの分類をする方法を紹介していきます。
scikit-learnの使い方に焦点を置くため、細かな理論は説明はしません。詳しく勉強したい人は以下の書籍が参考になります。SVMに関する内容は下巻に記載されています。上巻で、確率論や線形回帰、線形識別、ニューラルネットワークといったベースとなる内容が書かれているため、上巻を読んでからの方がより理解が進むかもしれません。私の場合は、大学の研究室で輪講という形で勉強して発表したりしていました。正直高い&難しい部類の本ですが、理解できると非常に価値がある書籍であると思います。
scikit-learnでサポートベクターマシン(SVM)を使用する方法
以降のプログラムでは、scikit-learnを使用します。インストールがされていない場合はpipでインストールしておいてください。
pip install scikit-learn
サポートベクターマシン(SVM)を使用した分類(sklearn.svm.SVC)
サポートベクターマシン(SVM)を使用した分類では、sklearn.svm.SVCを使用します。以降では、線形分類の例と非線形分類の例を紹介します。
線形分類
データを線形に分類する簡単な例でサポートベクターマシンを適用してみます。以下のサンプルプログラムを用いて紹介します。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
def show_svm_result(svm_model, ax=None):
"""SVMの結果を表示する
Args:
svm_model: SVM学習結果モデル
ax: axisの指定 (デフォルト: None)
"""
if ax is None:
ax = plt.gca()
n_grid = 50
xlim, ylim = ax.get_xlim(), ax.get_ylim()
x = np.linspace(xlim[0], xlim[1], n_grid)
y = np.linspace(ylim[0], ylim[1], n_grid)
ygrid, xgrid = np.meshgrid(y, x)
xygrid = np.vstack([xgrid.ravel(), ygrid.ravel()]).T
decision = svm_model.decision_function(xygrid).reshape(xgrid.shape)
# 境界線、マージンを表示
ax.contour(
xgrid,
ygrid,
decision,
colors="k",
levels=[-1, 0, 1],
linestyles=["--", "-", "--"],
alpha=0.5,
)
# サポートベクターを表示
ax.scatter(
svm_model.support_vectors_[:, 0],
svm_model.support_vectors_[:, 1],
s=100,
linewidth=1,
facecolor="none",
edgecolor="r",
label="Support Vector",
)
ax.legend()
ax.set_xlim(xlim)
ax.set_ylim(ylim)
def main():
"""メイン関数"""
np.random.seed(0)
# ===== データの生成
data, label = make_blobs(n_samples=100, centers=2, cluster_std=0.5)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="o")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")
# ===== サポートベクターマシンを用いた学習
model = SVC(kernel="linear", C=1.0e10)
model.fit(data, label)
print(model)
print(model.support_vectors_)
# ===== svmの結果表示
show_svm_result(model)
# 描画
plt.show()
if __name__ == "__main__":
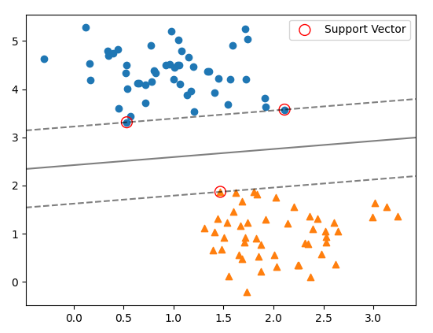
main()【実行結果】 SVC(C=10000000000.0, kernel='linear') [[0.5323772 3.31338909] [2.11114739 3.57660449] [1.46870582 1.86947425]]
【表示結果】
上記で紹介した実装例の細部について部分ごとに説明していきます。
必要モジュールのインポート
import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import make_blobs from sklearn.svm import SVC
サポートベクターマシンのSVMでの分類を実施するにはsklearn.svmからSVC(Support Vector Classification)をインポートします。また、対象データの生成用にsklearn.datasetsからmake_blobsをインポートしています。
データの用意
np.random.seed(0)
# ===== データの生成
data, label = make_blobs(n_samples=100, centers=2, cluster_std=0.5)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="o")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")SVMの分類対象となるデータを用意し、プロットしている部分です。make_blobsを使用すると簡単にサンプルデータが作成できます。今回指定しているのは以下のような引数です。値を変えたり、コメントアウトしたりして色々なデータで試してみてください。
- n_samples:データサンプル数
- centers:データ集合の中心の数
- cluster_std:各データ集合の標準偏差
乱数シードは上記例では、np.random.seedで設定していますが、make_blobsのrandom_state引数で指定することも可能です。
SVC(Support Vector Classification)の実行
# ===== サポートベクターマシンを用いた学習
model = SVC(kernel="linear", C=1.0e10)
model.fit(data, label)
print(model)
print(model.support_vectors_)上記が本題のサポートベクターマシンの学習を実行している部分です。今回は線形分類なので、kernelとして”linear”を指定してます。
Cはマージンの硬さをコントロールするためのパラメータです。Cが非常に大きな値の場合は、マージンは硬いためデータ点はマージンの中に入れません。一方で小さなCの場合はマージンは柔らかくなり、いくつかの点を包含することが可能になります(ソフトマージン)。SMVを実行しているのはfitメソッドです。
結果の可視化
show_svm_resultは、SVMの実行結果を可視化するため用に用意した関数になります。詳細は細かくは説明しませんが、SVMの境界線とサポートベクターを表示しています。
def show_svm_result(svm_model, ax=None):
"""SVMの結果を表示する
Args:
svm_model: SVM学習結果モデル
ax: axisの指定 (デフォルト: None)
"""
if ax is None:
ax = plt.gca()
n_grid = 50
xlim, ylim = ax.get_xlim(), ax.get_ylim()
x = np.linspace(xlim[0], xlim[1], n_grid)
y = np.linspace(ylim[0], ylim[1], n_grid)
ygrid, xgrid = np.meshgrid(y, x)
xygrid = np.vstack([xgrid.ravel(), ygrid.ravel()]).T
decision = svm_model.decision_function(xygrid).reshape(xgrid.shape)
# 境界線、マージンを表示
ax.contour(
xgrid,
ygrid,
decision,
colors="k",
levels=[-1, 0, 1],
linestyles=["--", "-", "--"],
alpha=0.5,
)
# サポートベクターを表示
ax.scatter(
svm_model.support_vectors_[:, 0],
svm_model.support_vectors_[:, 1],
s=100,
linewidth=1,
facecolor="none",
edgecolor="r",
label="Support Vector",
)
ax.legend()
ax.set_xlim(xlim)
ax.set_ylim(ylim)実行結果の確認
【実行結果(再掲)】 SVC(C=10000000000.0, kernel='linear') [[0.5323772 3.31338909] [2.11114739 3.57660449] [1.46870582 1.86947425]]
【表示結果(再掲)】

サポートベクターとして選択された点は「model.support_vectors_」で取得ができます。上記の例では、3点(0.5323772, 3.31338909)(2.11114739, 3.57660449)(1.46870582, 1.86947425)がサポートベクターとして選択されています。また、サポートベクターはマージンの境界線上にのっていることがわかるかと思います。
非線形分類
上記で見てきた分類例では、直線で分類できるような例でした。SVMは、カーネル法と組み合わせることで非線形な分類についても対応することができます。以下のサンプルプログラムを用いて紹介します。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_gaussian_quantiles
from sklearn.svm import SVC
def show_svm_result(svm_model, ax=None):
"""SVMの結果を表示する
Args:
svm_model: SVM学習結果モデル
ax: axisの指定 (デフォルト: None)
"""
if ax is None:
ax = plt.gca()
n_grid = 50
xlim, ylim = ax.get_xlim(), ax.get_ylim()
x = np.linspace(xlim[0], xlim[1], n_grid)
y = np.linspace(ylim[0], ylim[1], n_grid)
ygrid, xgrid = np.meshgrid(y, x)
xygrid = np.vstack([xgrid.ravel(), ygrid.ravel()]).T
decision = svm_model.decision_function(xygrid).reshape(xgrid.shape)
# 境界線、マージンを表示
ax.contour(
xgrid,
ygrid,
decision,
colors="k",
levels=[-1, 0, 1],
linestyles=["--", "-", "--"],
alpha=0.5,
)
# サポートベクターを表示
ax.scatter(
svm_model.support_vectors_[:, 0],
svm_model.support_vectors_[:, 1],
s=100,
linewidth=1,
facecolor="none",
edgecolor="r",
label="Support Vector",
)
ax.legend()
ax.set_xlim(xlim)
ax.set_ylim(ylim)
def main():
"""メイン関数"""
np.random.seed(0)
# ===== データの生成
data, label = make_gaussian_quantiles(n_samples=100, n_classes=2, n_features=2)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="o")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")
# ===== サポートベクターマシンを用いた学習
model = SVC(C=1.0e10)
model.fit(data, label)
print(model)
print(model.support_vectors_)
# ===== svmの結果表示
show_svm_result(model)
# 描画
plt.show()
if __name__ == "__main__":
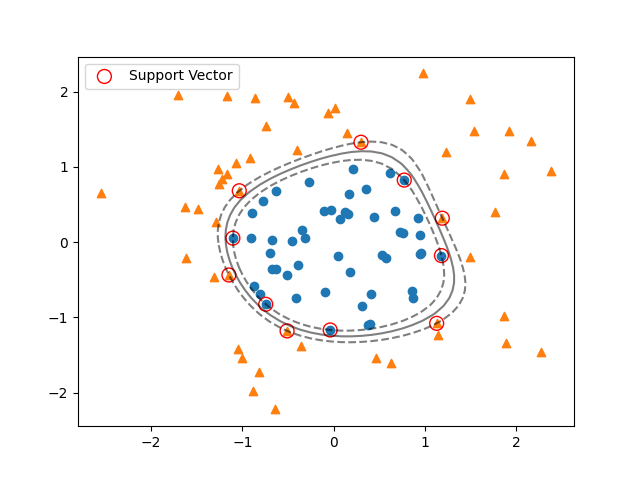
main()【実行結果】 SVC(C=10000000000.0) [[-0.74475482 -0.82643854] [-0.03928282 -1.1680935 ] [-1.10438334 0.05216508] [ 0.77179055 0.82350415] [ 1.17877957 -0.17992484] [ 1.12663592 -1.07993151] [-1.14746865 -0.43782004] [-1.03424284 0.68159452] [-0.51080514 -1.18063218] [ 1.18802979 0.31694261] [ 0.29823817 1.3263859 ]]
【表示結果】
上記で紹介した実装例の細部について部分ごとに説明していきます。線形分類で説明した部分と重複するような部分は省略します。
必要モジュールのインポート
from sklearn.datasets import make_gaussian_quantiles
線形では分類できないようなデータ生成用に、sklearn.datasetsからmake_gaussian_quantilesをインポートしています。
データの用意
np.random.seed(0)
# ===== データの生成
data, label = make_gaussian_quantiles(n_samples=100, n_classes=2, n_features=2)
plt.scatter(data[label == 0, 0], data[label == 0, 1], marker="o")
plt.scatter(data[label == 1, 0], data[label == 1, 1], marker="^")make_gaussian_quantilesを使用してサンプルデータを作成しています。今回指定しているのは以下のような引数です。値を変えたり、コメントアウトしたりして色々なデータで試してみてください。
- n_samples:データサンプル数
- n_classes:データ集合の数
- n_features:データの特徴数
乱数シードは上記例では、np.random.seedで設定していますが、make_gaussian_quantilesのrandom_state引数で指定することも可能です。
SVC(Support Vector Classification)の実行
# ===== サポートベクターマシンを用いた学習
model = SVC(C=1.0e10)
model.fit(data, label)
print(model)
print(model.support_vectors_)上記の部分がサポートベクターマシンを実行している部分です。今回、kernelを指定していませんが、デフォルトのrbf(動径基底関数)が指定されています。
明示的にkernel=’rbf’と指定しても構いません。Cについては、線形分類の説明でも説明した通りマージンの硬さをコントロールするパラメータです。
実行結果の確認
【実行結果(再掲)】 SVC(C=10000000000.0) [[-0.74475482 -0.82643854] [-0.03928282 -1.1680935 ] [-1.10438334 0.05216508] [ 0.77179055 0.82350415] [ 1.17877957 -0.17992484] [ 1.12663592 -1.07993151] [-1.14746865 -0.43782004] [-1.03424284 0.68159452] [-0.51080514 -1.18063218] [ 1.18802979 0.31694261] [ 0.29823817 1.3263859 ]]
【表示結果(再掲)】

結果表示には線形分類の時と同じ独自に作ったshow_svm_result関数を使用しています。結果を見てみると境界面が曲線になっているような分類ができていることが分かります。また、サポートベクターとしては11点が選択されていることが分かるかと思います。
この例のように、サポートベクターマシンは非線形な分類についても適用することが可能です。
まとめ
本記事では、Pythonの機械学習ライブラリであるscikit-learnを用いてサポートベクターマシン(SVM)を使ったデータの分類をする方法を紹介してきました。
SVM実行のためのコードは、非常に短いコードで実現できていることがお分かりいただけたかと思います。scikit-learnを用いるとSVMのような機械学習の実行が簡単に実現できます。是非色々と試してみていただければと思います。
sklearn.svm.SVCの公式ドキュメントの説明はこちらを参考にしてください。
上記で紹介しているソースコードについてはgithubにて公開しています。参考にしていただければと思います。
の使用方法.jpg)






を用いたデータ分類方法-640x360.jpg)


