【scikit-learn】k近傍法（k-NN）を用いたデータ分類方法

Pythonの機械学習ライブラリであるscikit-learnのKNeighborsClassifierを使ってk近傍法(k-NN)によるデータ分類を行う方法を解説します。

Contents

1 k近傍法（k-NN）
2 scikit-learnのKNeighborsClassifierを使ってk近傍法によるデータ分類をする方法
- 2.1 k近傍法の使い方（sklearn.neighbors.KNeighborsClassifier）
  - 2.1.1 実装例
  - 2.1.2 実装内容の解説
3 まとめ

k近傍法（k-NN）

k近傍法（k-NN）とは、分類の手法の一つです。分類の中では非常に単純なアルゴリズムにであり、他のアルゴリズムのように識別関数、識別モデル、生成モデルのようなものを学習するわけではないため、機械学習の中でも怠惰学習と呼ばれたりします。

k近傍法の概要を見てみましょう。k-NNは、k-Nearest Neighborsという名の通り、分類したい対象データからk個の近傍のデータ点を見つけて多数決によって分類するクラスを決めます。近傍を求める際の距離尺度としては、一般的には距離はユークリッド距離が使用されます。参考にですが、距離尺度には他にもマンハッタン距離やマハラノビス距離といったものがあります。

k近傍法の例を少し見てみましょう。以下のようなデータで黄色のデータ点が青なのか緑なのかを分類したいとしましょう。k=3とすると、青:1、緑:2となるので分類結果は緑となります。しかし、k=8とすると青:5、緑:3となるため青に分類されます。このようにいくつの近傍数を見るかによって分類結果は変わってきます。

k近傍法は、Pythonの機械学習ライブラリであるscikit-learnにてKNeighborsClassifierで実装がされています。本記事では、scikit-learnのKNeighborsClassifierを使ってk近傍法によるデータ分類する方法を紹介します。

scikit-learnのKNeighborsClassifierを使ってk近傍法によるデータ分類をする方法

以降では、scikit-learnを使用します。インストールがされていない場合はpipでインストールしておいてください。

pip install scikit-learn

k近傍法の使い方（sklearn.neighbors.KNeighborsClassifier）

実装例

scikit-learnのmake_classificationで生成したデータを使って、k近傍法を実現するKNeighborsClassifierの使い方を紹介します。k近傍法は、近傍数をいくつにするかで結果が変わるのでそれも比較してみようと思います。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


def main():
    """メイン関数"""
    np.random.seed(1)

    # ===== データの用意
    data, label = make_classification(
        n_samples=1000,
        n_classes=2,
        n_features=4,
        n_informative=4,
        n_redundant=0,
    )
    # データセットを訓練用、テスト用に分割する
    train_data, test_data, train_label, test_label = train_test_split(data, label)

    # ===== 複数のkで性能が分類性能がどのように変わるか確認
    k_list = [k for k in range(1, 11)]
    acc_list = []

    # ===== kを変えながらモデルを順番に学習
    for k in k_list:
        # モデルの構築
        model = KNeighborsClassifier(n_neighbors=k)
        # モデルの学習
        model.fit(train_data, train_label)
        # 正解率の評価
        acc_list.append(model.score(test_data, test_label))

    # ===== 正解率をプロットする
    plt.plot(k_list, acc_list)
    plt.title("accuracy list")
    plt.xlabel("n_neighbors")
    plt.ylabel("accuracy")
    plt.show()


if __name__ == "__main__":
    main()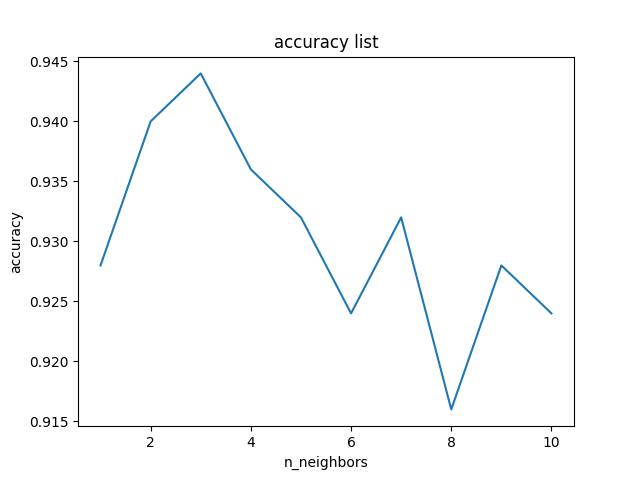

実装内容の解説

上記で紹介した実装例の各部分ごとに内容を紹介していきます。

必要モジュールのインポート

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

まずは、必要なモジュール類をインポートします。今回はscikit-learnのKNeighborsClassifierを使用するので、sklearn.neighborsからインポートします。またデータ生成用にmake_classification、データ分割のためにtrain_test_splitをインポートしています。numpyとmatplotlibはデータの操作や可視化用です。

データセットの準備

    np.random.seed(1)

    # ===== データの用意
    data, label = make_classification(
        n_samples=1000,
        n_classes=2,
        n_features=4,
        n_informative=4,
        n_redundant=0,
    )
    # データセットを訓練用、テスト用に分割する
    train_data, test_data, train_label, test_label = train_test_split(data, label)

データはmake_classificationを使って生成します。指定しているパラメータとしては以下のような項目です。

n_samples：データ点数
n_classes：データのクラス数
n_features：各データの次元数
n_infomative：各データで情報を持ってる特徴数
n_redundant：各データで冗長な特徴数

今回は4次元の特徴を持つ1,000点のデータで、2つのクラスに分かれているデータを生成します。

n_infomativeは4次元のうち意味のある特徴数で、n_redundantは冗長な特徴数という意味ですが、公式ドキュメントの記載を見ると「infomativeな特徴のランダムな線形結合で生成される特徴の数」ということです。他の特徴で表現できるということは情報はもっていないような特徴ということですね。

乱数シードは、np.random.seedで設定していますが、make_classificationのrandam_state引数で乱数シードを指定することも可能です。

あとは、train_test_splitを使ってデータを訓練用とテスト用に分割しています。

Note

make_classificationの公式ドキュメントはこちらを参考にしてください。

モデルの生成と正解率

    # ===== 複数のkで性能が分類性能がどのように変わるか確認
    k_list = [k for k in range(1, 11)]
    acc_list = []

    # ===== kを変えながらモデルを順番に学習
    for k in k_list:
        # モデルの構築
        model = KNeighborsClassifier(n_neighbors=k)
        # モデルの学習
        model.fit(train_data, train_label)
        # 正解率の評価
        acc_list.append(model.score(test_data, test_label))

上記部分がk近傍法を実行している部分です。まずは、KNeighborsClassifierをインスタンス化します。その際の引数としては近傍数のn_neighborsを指定します。

モデルの学習については、fitを使用してtrain_dataとtrain_labelを使用します。また、正解率は、訓練データとは異なるtest_dataとtest_labelを用いてscoreにより計算します。

今回はk=1~10までの数を順番に変えながらfor文で実行し、正解率をリストに追加していきます。

正解率のプロット

    # ===== 正解率をプロットする
    plt.plot(k_list, acc_list)
    plt.title("accuracy list")
    plt.xlabel("n_neighbors")
    plt.ylabel("accuracy")
    plt.show()

こちらの部分は、計算した正解率のリストをプロットしている部分です。正解率は、どうやらn_neighbors=3の時が最も高いようです。

もちろん今回のデータではという意味ですので、3が常に適切ということはありません。対象とする問題によりハイパーパラメータとして調整する必要があります。近傍数の数が多すぎると分類範囲の狭いようなカテゴリーではうまく分類されない場合もあります。

以上が、scikit-learnのKNeighborsClassifierを使ったk近傍法(k-NN)によるデータ分類方法の紹介でした。