正規分布間のKLダイバージェンス（Kullback-Leibler divergence）の導出
naoki-hn Python Tech
L1正則化とL2正則化の概要と効果
naoki-hn
機械学習の分野において汎化誤差を減少させる方法の 1 つである L1 正則化と L2 正則化について概要と効果についてまとめます。
過学習と正則化
機械学習では、モデルを決めたうえで学習データに対して学習を行い、テストデータを使ってモデルの評価をするということを行います。
テストデータは、学習時には未知のデータであり、このような未知のデータに対する誤差を小さくできるようなモデルが望ましいです。未知のデータに対してモデルを適用できるようにすることを汎化と言い、未知のデータに対する誤差を汎化誤差と言います。
ただし、機械学習ではよく学習データに過度にモデルが適合してしまう過学習という現象が起こります。過学習では、学習データに対する誤差は非常に小さくなるのですが、未知のデータであるテストデータに対する汎化誤差は大きくなってしまいます。
過学習発生しないようにして、汎化誤差を減少させる目的で学習のアルゴリズムに適用する変更の事を正則化と言います。この記事では、正則化でよく用いられる方法であるL1 正則化と L2 正則化について、数式の意味や効果について紹介していきます。
L1 正則化と L2 正則化の概要と効果
以降では、L1 正則化と L2 正則化の式を紹介しつつ、数式の図的な意味とその効果について説明していきます。なお、以降では、損失関数を $\mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}})$、正則化を加えた目的関数 $\mathrm{R}$ と表現することとします。
L1 正則化
L1 正則化項を損失関数に加えた目的関数 $\mathrm{R}_{l1}$ は、以下の式のように表すことができます。なお、$\alpha$ は正則化項の影響の度合いを決定するハイパーパラメータで自分で決める必要があります。
\[
\mathrm{R}_{l1} = \mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}}) + \alpha\sum_{i=0}^{n}|w_{i}|
\]
L1 正則化項は、機械学習のモデルの重みパラメータの絶対値の和となっています。モデルを最適化する場合には、$\mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}})$ を最小化するのではなく、正則化項を加えた $\mathrm{R}_{l1}$ を最小化します。
L1 正則化は、数式を見ると分かるようにパラメータの値 $\boldsymbol{w}$ が大きくなると目的関数が大きくなってしまうため、$\boldsymbol{w}$ が大きくならないように制約をかけているという意味になります。
L1 正則化と後述する L2 正則化では、制限のかかり方が異なっており、それが性質の違いに現れます。では、L1 正則化がどのような効果を持っているのかについて以下の図を見ながら確認しましょう。この図はよく L1 正則化の説明で出てくる図です。
簡単のためにパラメータは $w_{1}$ と $w_{2}$ の 2 つとします。
オレンジの円は損失関数 $\mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}})$ の等高線だと思ってください。同じ線上では $\mathrm{E}$ の値は同じで円の内側ほど損失関数の値は小さいものとします。
また、青い線は L1 正則化項の等高線です。例えば $w_{1}+w_{2}=c$ ($c$ は定数) となるような線が図中のそれぞれの線になります。
この図を見たときに損失関数と正則化項を足した関数 $\mathrm{R}_{l1}$ が最小になる点を考えると損失関数と正則化項の等高線が接するような赤い点が最小です。なぜなら、上記図で同じ損失関数の値である円上の点のうち、正則化項が最小となるのはひし形を徐々に拡大していったときに、はじめて楕円と接する点であるためです。
ここでポイントは、損失関数と接する点では、上記の例では $w_{1}$ が 0 となるということです。このため、L1 正則化は、重要なパラメータをそのまま残して不要なパラメータを 0 にする効果があります。このような状況をスパースであると言います。
L2 正則化
L2 正則化項を損失関数に加えた目的関数 $\mathrm{R}_{l2}$ は、以下の式のように表すことができます。なお、$\alpha$ は正則化項の影響の度合いを決定するハイパーパラメータで自分で決める必要があります。
\[
\mathrm{R}_{l2} = \mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}}) +\alpha\sum_{i=0}^{n}w_{i}^{2}
\]
L2 正則化項は、機械学習のモデルの重みパラメータの 2 乗の和となっています。モデルを最適化する場合には、$\mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}})$ を最小化するのではなく、正則化項を加えた $\mathrm{R}_{l2}$ を最小化します。
L2 正則化は、L1 正則化と同じように $\boldsymbol{w}$ が大きくなると目的関数が大きくなってしまうため、$\boldsymbol{w}$ が大きくならないように制約をかけるという意味があります。
では、L2 正則化がどのような効果を持っているのかについて、L1 正則化の時と同じように図を見ながら確認しましょう。この図はよく L2 正則化の説明で出てくる図です。
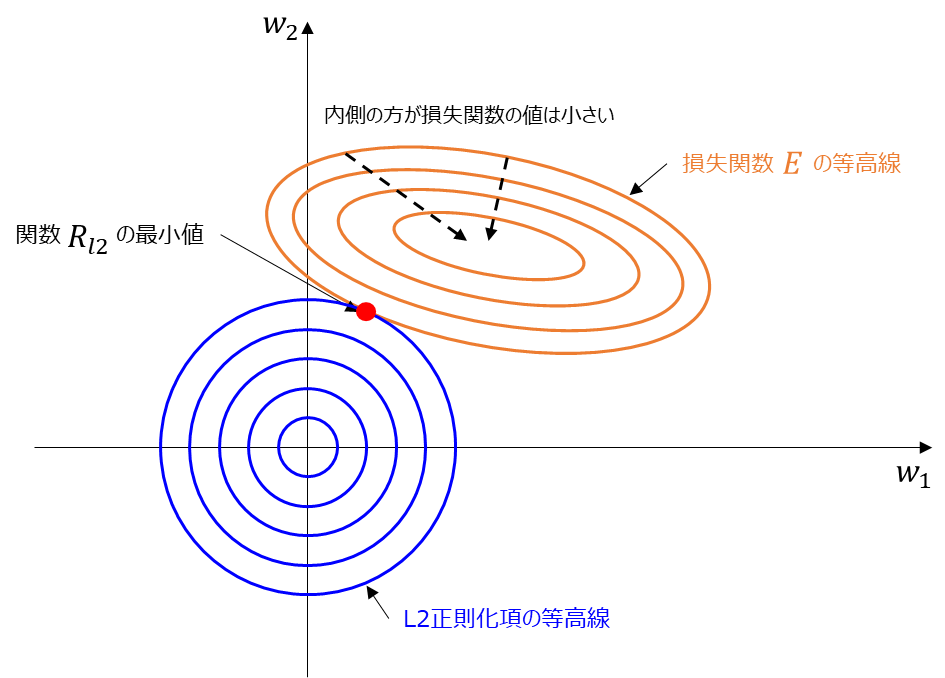
簡単のためにパラメータは $w_{1}$ と $w_{2}$ の 2 つとします。
オレンジの円は損失関数 $\mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}})$ の等高線です。同じ線上では $\mathrm{E}$ の値は同じで、円の内側に行くほど損失関数の値は小さいものとします。
また、青い線は L2 正則化項の等高線です。例えば $w_{1}^{2}+w_{2}^{2}=c$ ($c$ は定数) となるような線がそれぞれの円というようになります。
この図を見たときに、損失関数と正則化項を足した関数 $\mathrm{R}_{l2}$ が最小になる点を考えてみると損失関数と正則化項の等高線が接するような赤い点が最小です。なぜなら、上記図で同じ損失関数の値である円上の点のうち、正則化項が最小となるのは円を徐々に拡大していったときに、はじめて楕円と接する点であるためです。
ここでポイントは、L2 正則化は、パラメータを全体的に小さくする効果があります。L1 正則化のように 1 部のパラメータを 0 に近づけるような効果はない点を覚えておきましょう。
まとめ
機械学習の分野において汎化誤差を減少させる方法の 1 つである L1 正則化と L2 正則化について概要と効果をまとめました。
L1 正則化と L2 正則化のそれぞれについて図的な意味についても紹介しています。それぞれの正則化の数式と効果をまとめてみると以下の通りです。
| 正則化 | 数式 | 効果 |
|---|---|---|
| L1 | $ \mathrm{R}_{l1} = \mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}}) + \alpha\sum_{i=0}^{n}|w_{i}| $ | 重要なパラメータをそのまま残して不要なパラメータを 0 にする効果がある (スパース) |
| L2 | $ \mathrm{R}_{l2} = \mathrm{E}(\boldsymbol{y}, \hat{\boldsymbol{y}}) +\alpha\sum_{i=0}^{n}w_{i}^{2} $ | パラメータを全体的に小さくする効果がある |
L1 正則化も L2 正則化もパラメータが大きくならないように制約をかけるという点では同じですが、効果には特徴の違いがあります。よく効果の特徴を理解した上でモデルへの適用を検討してみてください。
あわせて読みたい
【Python Tech】プログラミングガイド
ABOUT ME
はじめまして。当サイトをご覧いただきありがとうございます。
私は製造業のメーカーで、DX推進や業務システムの設計・開発・導入を担当しているシステムエンジニアです。これまでに転職も経験しており、以前は大手電機メーカーでシステム開発に携わっていました。
プログラミング言語はこれまでC、C++、JAVA等を扱ってきましたが、最近では特に機械学習等の分析でも注目されているPythonについてとても興味をもって取り組んでいます。これまでの経験をもとに、Pythonに興味を持つ方のお役に立てるような情報を発信していきたいと思います。どうぞよろしくお願いいたします。
※キャラクターデザイン：ゼイルン様
プログラミング言語はこれまでC、C++、JAVA等を扱ってきましたが、最近では特に機械学習等の分析でも注目されているPythonについてとても興味をもって取り組んでいます。これまでの経験をもとに、Pythonに興味を持つ方のお役に立てるような情報を発信していきたいと思います。どうぞよろしくお願いいたします。
※キャラクターデザイン：ゼイルン様