【TensorFlow】GradientTapeの自動微分による勾配の計算方法

Googleによって開発されている機械学習ライブラリであるTensorFlowで、GradientTapeを使った自動微分による勾配の計算方法について解説します。
目次
自動微分による勾配の計算 (GradientTape)
TensorFlowは、NumPyに非常によく似た使用方法で使用することができます。では、どういった点が違うのでしょうか。TensorFlowには、NumPyにはできない重要な機能があります。それは、微分可能な式の勾配を入力のいずれかの変数に基づいて自動で計算する機能です。
勾配の自動計算は自動微分(automatic differentiation、またはautodiff)と呼ばれます。
TensorFlowで実装されているのはリバースモードの自動微分というものです。ディープラーニングでは計算グラフというものが重要になりますが、まずはフォワードで入力から出力の方向に計算グラフを計算し、次に逆方向で出力から入力の方向にグラフをたどって偏微分を計算します。リバースモードというのはこの逆方向にたどりながら微分を計算することに由来します。
TensorFlowでは、この自動微分による勾配計算をする方法として、GradientTapeというAPIを備えています。本記事では、GradientTapeの基本的な使い方について紹介していきます。
GradientTapeの基本的な使い方
TensorFlowのGradientTapeを用いた自動微分は以下のように使用します。
import tensorflow as tf
x = tf.Variable(5.0)
# フォワード計算
with tf.GradientTape() as tape:
result = tf.square(x)
# リバースモードの自動微分を計算
gradient = tape.gradient(result, x)
print(gradient)【実行結果】 tf.Tensor(10.0, shape=(), dtype=float32)
まずは、入力から出力の計算をするフォワード計算をします。その際には、with句を使ってGradientTape()を用意します。上記例ではtapeとして用意しており、このtapeに計算の過程が記録されて、後ほど微分を計算する際に使用することになります。
with句の中ではフォワード計算を記載していきます。今回の例では、tf.squareということで$y=x^{2}$の計算をしています。xには5が入っているので、resultとしては25となります。
リバースモードとして自動微分を行う際には、tapeのgradientメソッドに計算結果(今回はresult)と微分対象の変数(今回はx)を指定します。上記例での結果は10となっていることが分かります。$y=x^{2}$は微分してみると$\frac{dy}{dx}=2x$となるので、$x=5$を代入してみると$10$になることが分かります。
上記例は、非常に簡単な例なので数式を微分して代入すればいいではないかと思うかもしれません。その通りなのですが、実際にディープラーニングで作られる計算グラフ計算は非常に複雑になり手計算で求めるのはとても大変です。複雑な計算グラフの場合でも微分が求められてしまうのがGradientTapeが非常に強力な点です。
定数Tensorの場合
定数Tensorは追跡されない
上記でGradientTapeの基本的な使い方を見てきましたが、変数はtf.Variableを使用していました。定数テンソルの場合は、以下のようにGradientTapeでは追跡されず微分を計算してもNoneとなってしまいます。
import tensorflow as tf
x = tf.constant(5.)
# フォワード計算
with tf.GradientTape() as tape:
result = tf.square(x)
# リバースモードの自動微分を計算(定数だと追跡されない)
gradient = tape.gradient(result, x)
print(gradient)【実行結果】 None
定数Tensorの追跡方法 tape.watch()
定数テンソルの場合でGradientTapeによる計算の追跡をしたい場合には、以下のようにtape.watchメソッドにより追跡対象を明確に指定する必要があります。
import tensorflow as tf
x = tf.constant(5.0)
# フォワード計算
with tf.GradientTape() as tape:
# 追跡対象の定数を明確に指定する
tape.watch(x)
result = tf.square(x)
# リバースモードの自動微分を計算(定数でも計算できる)
gradient = tape.gradient(result, x)
print(gradient)
【実行結果】 tf.Tensor(10.0, shape=(), dtype=float32)
結果を見てみると定数のxに対して微分が計算できていることが分かるかと思います。
具体例:GradientTapeによる勾配計算
これまでにGradientTapeの基本的な使い方を見てきましたが、具体的な例を使って計算の例を見てみましょう。
簡単な計算グラフの問題
計算グラフの勉強・理解には書籍「ゼロから作るDeep Learning」がおすすめできます。この書籍で例題として挙げられているスーパーでの買い物の例を引用・使用させていただいてGradientTapeによる勾配計算をしてみましょう。
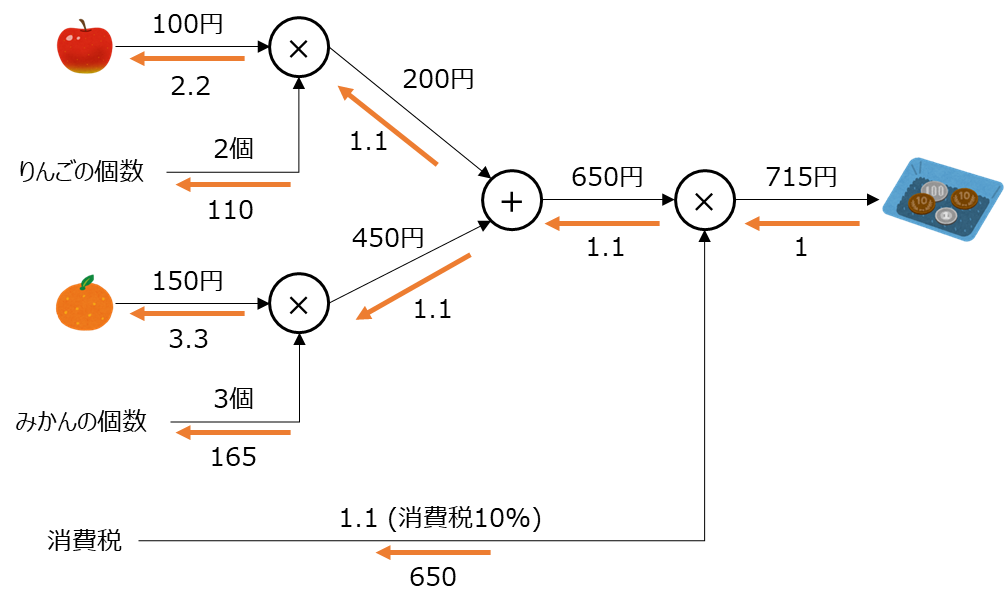
この例では、りんご2個とみかん3個を購入して支払う金額を計算している簡単な例です。左が入力、右が出力で、左から右に向かう矢印はフォワードの計算処理を表しています。逆方向のオレンジ色の矢印が逆伝播して勾配を計算している流れです。
計算グラフの説明が主目的ではないので詳細は割愛しますが、見方を簡単に説明します。例えば、りんごの部分は「2.2」という数値になっています。これは「りんごの値段に対する支払金額の微分」です。つまり、りんごが1円値上がりすると、支払金額は2.2円増えることを意味します。もう少し正確に言うと、りんごの値段が微小な値変化した場合、その微小な値×2.2倍だけの金額が支払金額に加算されるということです。
この例の微分値をTensorFlowのGradientTapeを使って計算してみましょう。具体的なプログラムとしては以下のようになります。
import tensorflow as tf
# りんごの価格
apple = tf.Variable(100.0)
# りんごの個数
apple_num = tf.Variable(2.0)
# みかんの価格
orange = tf.Variable(150.0)
# みかんの個数
orange_num = tf.Variable(3.0)
# 消費税
tax = tf.Variable(1.1)
# フォワード計算
with tf.GradientTape() as tape:
apple_val = apple * apple_num
orange_val = orange * orange_num
sum_val = apple_val + orange_val
payment = tax * sum_val
print(f"支払金額: {payment}", "\n")
# 勾配計算(リバースモード)
grads = tape.gradient(payment, [apple, apple_num, orange, orange_num, tax])
for grad in grads:
print(grad)【実行結果】 支払金額: 715.0 tf.Tensor(2.2, shape=(), dtype=float32) tf.Tensor(110.0, shape=(), dtype=float32) tf.Tensor(3.3000002, shape=(), dtype=float32) tf.Tensor(165.0, shape=(), dtype=float32) tf.Tensor(650.0, shape=(), dtype=float32)
上記の例では、各入力をそれぞれtf.Variableの変数として作成しています。
tf.GradientTape()のwith句の中がフォワード計算になるので、その中で上記例の計算グラフ計算を行います。paymentに計算された値を見ても715円ということでちゃんと計算できていることが分かります。
次に、勾配を計算するためにtapeのgradientメソッドを呼び出し、計算結果のpaymentと偏微分の勾配を求める変数を渡します。今回は複数変数の偏微分を求めたいため、変数はリスト形式で渡しています。
偏微分結果はリストで返ってくるため、順次取り出して計算結果を表示していますが、上記図の手計算の結果と一致していることが分かるかと思います。TensorFlowでは、GradientTapeを使ってこのような計算手順を実行することで簡単に勾配を求めることができます。上記は簡単な例ですがより複雑な計算グラフも同様に自動計算してくれます。
フォワード計算はまとめて記載してよい
上記の説明では、計算グラフでの手順と対応させるために一つずつ丁寧に計算式を記載しましたが、以下のようにまとめて計算式を書いて問題ありません。
# フォワード計算
with tf.GradientTape() as tape:
payment = tax * (apple * apple_num + orange * orange_num)
print(f"支払金額: {payment}", "\n")フォワード計算は関数化することも可能
フォワード計算は、以下のように関数化しても同様の結果が得られます。
@tf.function
def calc_payment(apple, apple_num, orange, orange_num, tax):
return tax * (apple * apple_num + orange * orange_num)
# フォワード計算
with tf.GradientTape() as tape:
payment = calc_payment(apple, apple_num, orange, orange_num, tax)
print(f"合計: {payment}", "\n")関数には@tf.functionデコレータをつけていますが、これはPythonの関数をTensorFlowにあわせて最適化してくれるものです。なお、@tf.functionの記載がなくでも上記のコードは動作します。
以上が、TensorFlowにおけるGradientTapeによる自動微分の方法でした。
まとめ
Googleによって開発されている機械学習ライブラリであるTensorFlowで、GradientTapeを使った自動微分による勾配の計算方法について解説しました。
TensorFlowはNumPyに似た使い方ができますが、NumPyにできない機能として自動微分(automatic differentiation、またはautodiff)があります。TensorFlowで実装されているのはリバースモードという自動微分で、フォワード計算をした後に逆伝播して微分を求めます。
TensorFlowでは、自動微分の仕組みとしてGradientTapeというAPIを備えています。この記事ではGradientTapeの基本的な使い方を簡単な例を用いて紹介しました。
ディープラーニングで、より複雑な計算をする際の基礎となりますので、GradientTapeの使い方についてしっかり理解してもらうとよいかなと思います。
上記で紹介しているソースコードについてはgithubにて公開しています。参考にしていただければと思います。








の実装.jpg)