因果推論における因果ダイアグラムにおいて重要な構造であるチェーン、フォーク、コライダーの概要と特徴について解説します。
Contents
因果ダイアグラムで重要な構造
因果推論において因果ダイアグラム（Causal Diagram）は因果関係を視覚的に表現するための重要なツールです。因果ダイアグラムや基本的なグラフの概要については「因果ダイアグラムの概要」でまとめているので参考にしてください。
因果ダイアグラムにおいては理解しておくべき非常に重要な３つの基本構造が「チェーン」「フォーク」「コライダー」です。これらの特徴を押さえておくことは因果推論の技術を理解する上で役立ちます。
この記事ではチェーン、フォーク、コライダーの構造に関する概要を紹介するとともに、各構造から生成したデータで特徴を見ていきたいと思います。
因果推論では、因果のはしごという重要な概念があります。因果のはしごについては「因果のはしごの概要」でまとめているので参考にしてください。
チェーン
チェーン（Chain）は因果関係が連続的に伝わる構造です。グラフで表現すると以下のようになります。
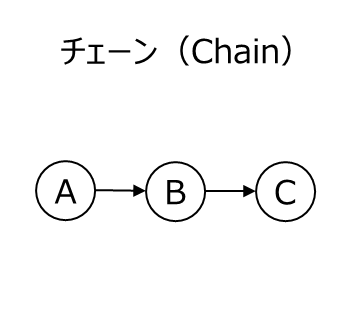
チェーン構造では、AがBに影響を与え、BがCに影響を与えます。Bは媒介変数（mediator）として機能します。この構造の特徴は、Bを条件付けるとAとCの間の統計的な関係が消え、統計的には独立となります。ただし、因果的な関係が消えたわけではなくBを介した影響は依然として存在します。
チェーン構造の例としてよく使用されるのは自動車の衝突警報システムです。「A:障害物」→「B:検知器」→「C:警報」というように、障害物があることで検知器が反応し、検知器が反応したら警報が鳴るというところにチェーン構造の因果関係があります。
フォーク
フォーク（Fork）は、一つの原因が複数の結果に影響を与える構造です。グラフで表現すると以下のようになります。
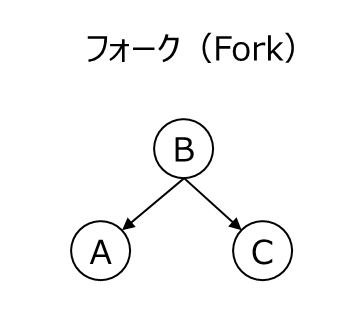
フォーク構造では、AとCの間に直接の因果関係はありませんが、共通の原因Bを通じて統計的な相関が生じる可能性があります。この相関は因果関係ではなく、単に共通の原因Bが両方に影響を与えているために生じます。
フォーク構造の例としてよく挙げられるのはアイスクリームの売上と溺死数の関係です。「A:アイスクリームの売上」、「C:溺死数」とすると、これらの間には相関があるように見えることがありますが、実際には直接的な因果関係はありません。
その背景には共通の原因として「B:気温」が存在すると考えられます。暑い季節になると、人々が海やプール等へ行く機会が増え、結果として溺死数が増加する可能性があり、また暑いことでアイスクリームを買う人も増える可能性があります。
交絡は様々なデータ分析で起こり得るため、何が何に関連しているかという因果ダイアグラムが事象を理解するために非常に重要になります。
コライダー
コライダー（Collider）は、複数の原因が一つの結果に影響を与える構造です。グラフで表現すると以下のようになります。
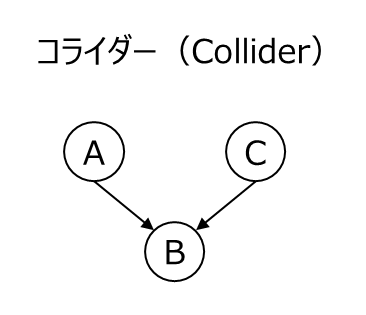
コライダー構造では、AとCがそれぞれBに影響を与えますが、AとCの間には相関も因果関係も存在しません。通常、AとCの間には相関も因果関係も存在しません。しかし、Bを条件付けるとAとCの間に見かけ上の相関が生じる可能性があります。ただし、この相関の強さは発生の有無はデータの分布によって異なります。
コライダーの例としては、就職活動で「A:能力」と「C:コネ」は、それぞれ「B:採用」に影響を与えます。ただし、能力とコネ自体は直接の因果関係を持ちません。しかし、Bの採用を条件付けた場合、能力とコネの間に相関が現れることがあります。例えば、採用された応募者の中ではコネが強い人は能力が低く、逆に能力が高い人はコネが弱いと見える場合があるためです。この相関の強さや方向（正の相関か負の相関か）はデータの分布に依存します。
このようにコライダーを条件付けると本来独立だった変数の間に見かけ上の相関が発生する場合があることに注意が必要です。ただし、必ず相関が発生するとは限りません。
Pythonでの各構造データ生成と回帰分析
上記で因果ダイアグラムの構造として重要な「チェーン」「フォーク」「コライダー」の概要や特徴を紹介しました。これらのデータ構造を持つデータをPythonで生成し、回帰分析することでそれぞれの特徴を確認してみたいと思います。
チェーンのデータセット
A → B → Cというチェーン構造に基づくデータを生成して回帰分析を行います。回帰分析ではstatsmodelsを使用し、CをAとBで回帰分析しています。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
# 乱数のシード設定
np.random.seed(42)
# Chainデータ生成 A -> B -> C
n = 1000
A = np.random.normal(0, 1, n)
B = 2 * A + np.random.normal(0, 1, n)
C = 3 * B + np.random.normal(0, 1, n)
# DataFrameを作成
chain_data = pd.DataFrame({"A": A, "B": B, "C": C})
# 回帰分析
# 定数項を追加
X = sm.add_constant(chain_data[["A", "B"]])
y = chain_data["C"]
model = sm.OLS(y, X).fit()
print(model.summary())
# データ可視化
plt.figure(figsize=(15, 5))
plt.suptitle("Chain Dataset")
# --- A vs B
plt.subplot(1, 3, 1)
plt.scatter(chain_data["A"], chain_data["B"], alpha=0.5)
plt.grid(True, linestyle="--", alpha=0.7)
plt.title("A vs B")
plt.xlabel("A")
plt.ylabel("B")
# --- B vs C
plt.subplot(1, 3, 2)
plt.scatter(chain_data["B"], chain_data["C"], alpha=0.5)
plt.grid(True, linestyle="--", alpha=0.7)
plt.title("B vs C")
plt.xlabel("B")
plt.ylabel("C")
# --- A vs C
plt.subplot(1, 3, 3)
plt.scatter(chain_data["A"], chain_data["C"], alpha=0.5)
plt.grid(True, linestyle="--", alpha=0.7)
plt.title("A vs C")
plt.xlabel("A")
plt.ylabel("C")
plt.tight_layout()
plt.show()
【実行結果】
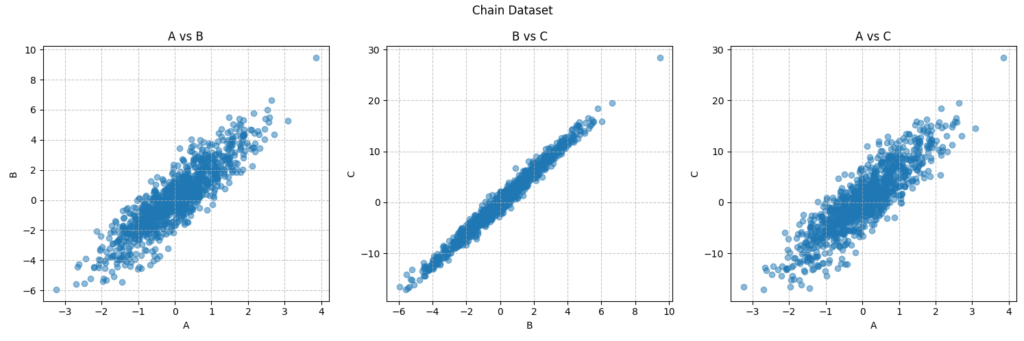
データのプロット結果を見るとAとB、BとC、AとCそれぞれで正の相関があるように見ることができます。
フォークのデータセット
A ← B → Cというフォーク構造を持つデータを生成し、チェーンの場合と同様に回帰分析を行います。データの可視化や回帰分析はチェーンの場合と同様で実行できるためデータ生成部分のみ以下に示します。
# 乱数のシード設定
np.random.seed(42)
# Forkデータ生成 A <- B -> C
n = 1000
B = np.random.normal(0, 1, n)
A = 2 * B + np.random.normal(0, 1, n)
C = 3 * B + np.random.normal(0, 1, n)
# DataFrameを作成
fork_data = pd.DataFrame({"A": A, "B": B, "C": C})【実行結果】
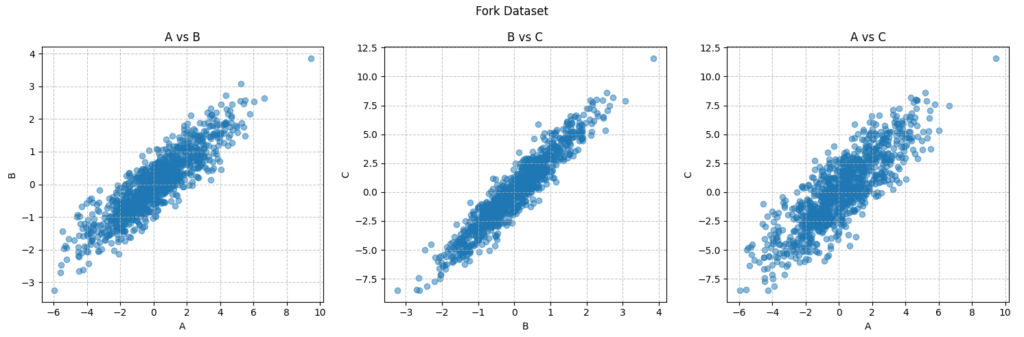
データのプロット結果を見るとチェーン構造と似たようにAとB、BとC、AとCそれぞれで正の相関があるように見えます。
コライダーのデータセット
A → B ← Cというコライダー構造を持つデータを生成し、チェーンの場合と同様に回帰分析を行います。データの可視化や回帰分析はチェーンの場合と同様で実行できるためデータ生成部分のみ以下に示します。
# 乱数のシード設定
np.random.seed(42)
# Colliderデータ生成 A -> B <- C
n = 1000
A = np.random.normal(0, 1, n)
C = np.random.normal(0, 1, n)
B = 2 * A + 3 * C + np.random.normal(0, 1, n)
# DataFrameを作成
collider_data = pd.DataFrame({"A": A, "B": B, "C": C})実行結果
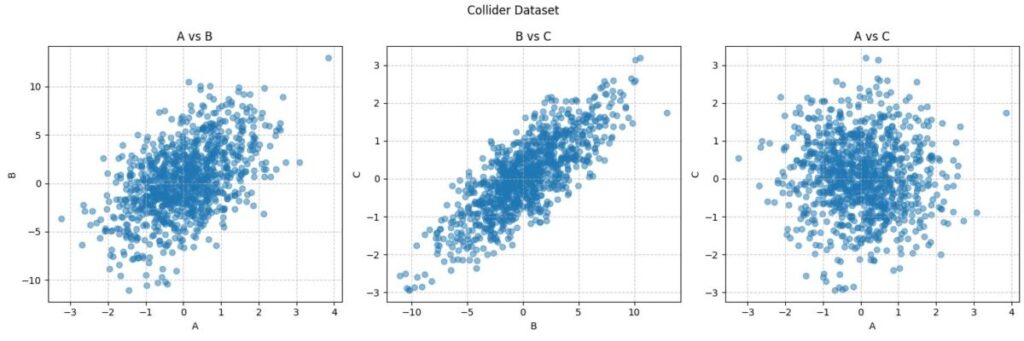
データのプロット結果を見るとチェーンやフォークと少し違った傾向がみられます。AとBやBとCについては正の相関があるように見えますが、AとCに関しては相関はないように見えます。
各データセットに対する回帰分析結果の考察
上記で各データセットを生成して変数ごとにプロットしてみつつ、回帰分析をしてみました。データの因果ダイアグラムが分かったうえでデータプロットを見てみると当たり前のように感じたかと思います。
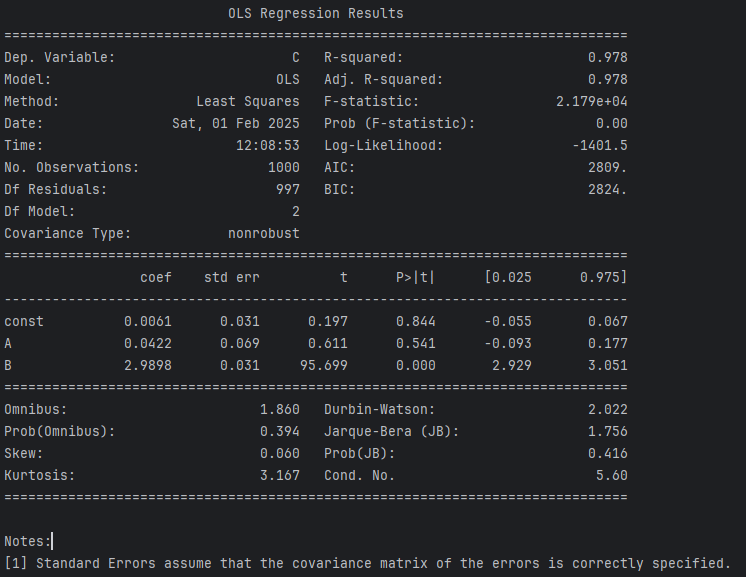
ここでは、回帰分析の統計的結果を少し深堀をしてみていきたいと思います。以下は、各回帰分析のサマリでprint(model.summary())の部分で表示されている結果です。
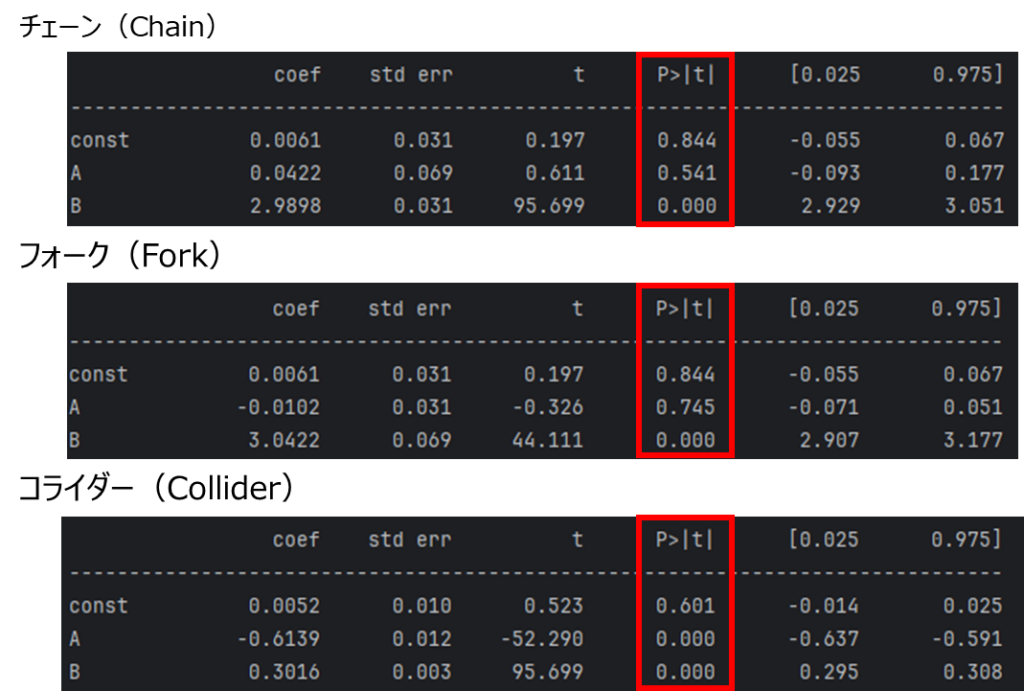
CについてAとBを用いて説明するための係数がcoefです。注目したいのは「P > |t|」の部分です。この値は、統計的仮説検定におけるt検定のp値を示しており、通常の閾値の0.05を使用すると、0.05以下のp値の場合は結果が統計的に有意であることを示しています。この値について各構造での結果を見てみましょう。
チェーン
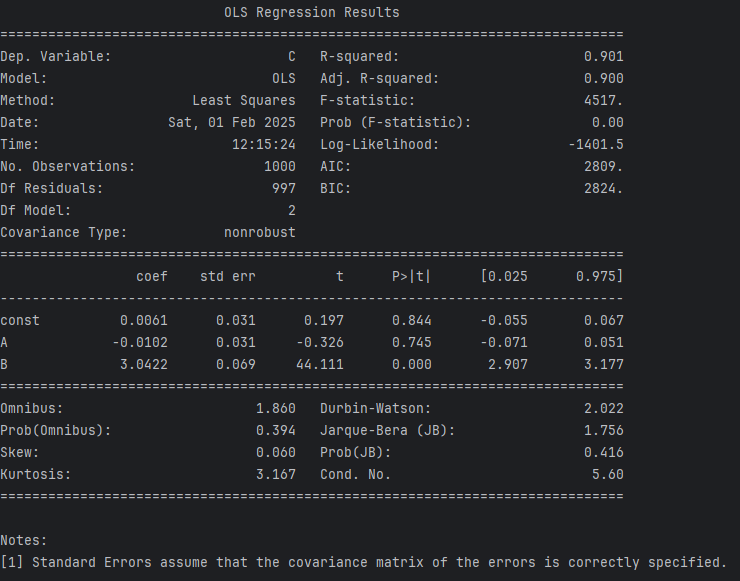
チェーン構造の結果のBの行を見るとP > |t|の値は、0.000で有意ですが、Aの行を見ると0.5であるため有意ではありません。つまり、AはCを説明するのに影響を与えていません。
Aが有意ではない理由は、Bを回帰モデルに含めるとAの影響は既にBにより説明されてしまうためです。つまり、BがCに強く影響を与えており統計的に有意であり、Aの影響はBによって説明されるため直接的には有意ではなくなったということです。
チェーン構造の概要で説明をした「Bを条件付けるとAとCの間の統計的な関連が消えて独立となる」という特徴と一致します。一方で、AとCのみで回帰分析してみると分かりますが、その場合はAは有意となります。
フォーク
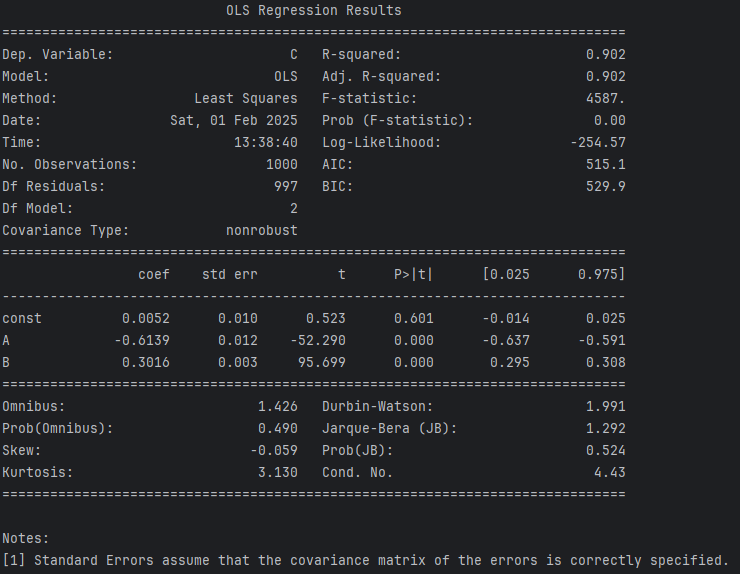
フォーク構造の結果では、Bは有意ですが、Aは有意ではありません。フォーク構造では、Bを条件付けすることでAとCの関係はなくなります。データプロットを見るとAとCの間に相関関係があるように見えますが、Bがモデルに入ることによって統計的な関係性がなくなるわけです。
このことは、交絡の原因となるBを条件付けすることが正確な分析をするために重要であることを示しています。
コライダー
コライダー構造の結果では、AとBの両方がCを説明するにあたって有意であるという結果となっています。コライダー構造の概要で説明した通り、コライダーではBを条件付けすると、AとCの間に見かけの相関が生じる可能性があります。
データプロットではAとCの間に関係ないであろうことが見て取れましたが、Bをモデルに含めたことによってAとCの間に見かけ上の相関が生じたわけです。
上記で見てきた通り、因果ダイアグラムの代表的な構造と統計的な分析結果との関係性を把握することは因果推論において非常に重要になってきます。
まとめ
因果推論における因果ダイアグラムにおいて重要な構造であるチェーン、フォーク、コライダーの概要と特徴について解説しました。各構造では以下のような特徴があります。
| 種類 | 構造 | 特徴 |
|---|---|---|
| チェーン（Chain） | A → B → C | Bを条件付けるとAとCは独立になる。 |
| フォーク（Fork） | A ← B → C | Bを条件付けするとAとCの統計的関係は消える。 |
| コライダー（Collider） | A → B ← C | Bを条件付けるとAとCの間に見かけの相関が発生する可能性がある。 |
因果推論では、因果ダイアグラムにおける因果関係と統計的な相関を理解することが重要です。
