2025.02.01 2025.11.23

【因果推論】因果ダイアグラムの概要

naoki-hn

因果推論では、因果ダイアグラムという因果関係を用いたモデルが重要になります。因果関係のグラフ構造を理解するための基本的な知識について解説します。

1 因果ダイアグラムとは
2 まとめ

因果ダイアグラムとは

因果ダイアグラムとは、変数間の因果関係を視覚的に表現するためのツールであり、因果推論において非常に重要な役割をします。特に、因果関係の構造を理解し、適切な介入や分析を設計する際に役立ちます。例えば、因果ダイアグラムを用いることで、ある要因が結果にどのように影響を与えるかを明確に表現できます。

この記事では、因果ダイアグラムを理解するために必要な基本的なグラフの概念と Python を用いた具体的な表現方法について解説します。

因果推論では、因果のはしごという重要な概念があります。因果のはしごについては「因果のはしごの概要」でまとめているので参考にしてください。

因果推論の科学「なぜ？」の問いにどう答えるか

posted with ヨメレバ

ジューディア・パール/ダナ・マッケンジー/松尾豊/夏目大文藝春秋 2022年09月12日頃

楽天ブックス

Amazon

因果ダイアグラムの理解に必要なグラフの概念

因果ダイアグラムを正しく理解するためには、まずグラフの基本的な概念について理解を深めておく必要があります。

グラフとは、ノード（頂点）とエッジ（辺）を持った構造のことで因果推論などに限らず様々な分野で利用されています。以降では、グラフの特徴として押さえておくべき事項について説明します。

有向グラフと無向グラフ

種類	概要
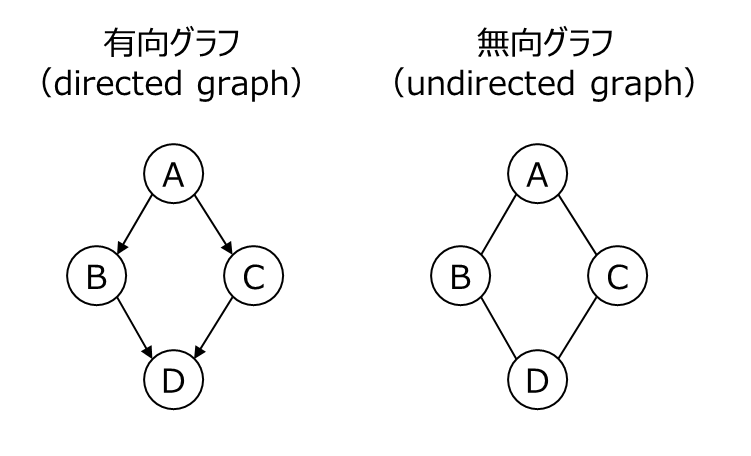
有向グラフ（directed graph）	ノード間のエッジに方向性があるグラフのことです。例えば、A → B は「A が B に影響を与える」という意味を持ちます。
無向グラフ（undirected graph）	ノード間のエッジに方向性がないグラフです。例えば A ー B は「A と B が関連している」という意味を持ちます。

巡回グラフと非巡回グラフ

種類	概要
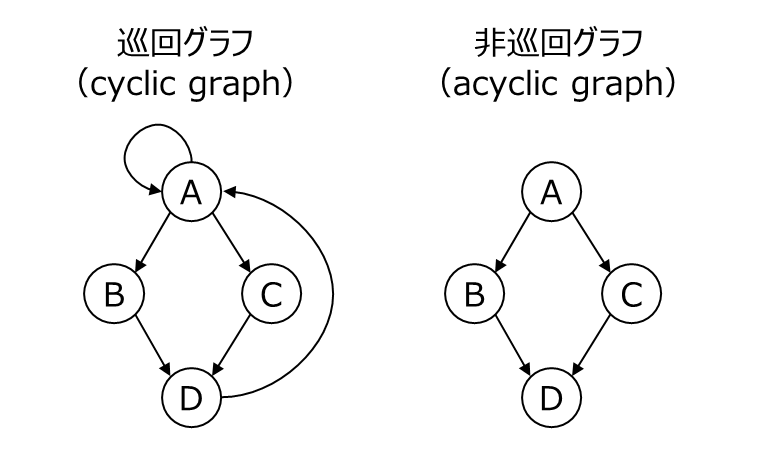
巡回グラフ（cyclic graph）	ノードをいくつかたどると、元のノードに戻ることができるパスを持つグラフです。
非巡回グラフ（acyclic graph）	元のノードに戻ってくることができるパスが存在しないグラフです。

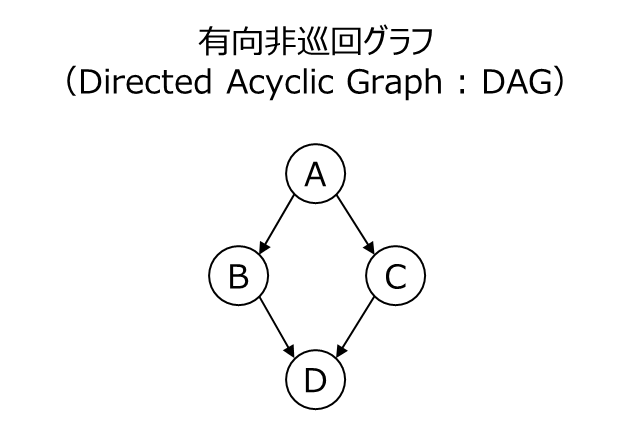
有向非巡回グラフ（Directed Acyclic Graph：DAG）

因果ダイアグラムにおいて特に重要なグラフとして有向非巡回グラフ（Directed Acyclic Graph：DAG）があります。このグラフは、有向グラフでありながら、どのノードからも自身に戻る経路を持たないグラフです。

この性質により、因果関係を時間準や論理的な順序に従って表現することができます。

因果ダイアグラムにおける構造パターン

因果ダイアグラムでは、変数間の関係性を表すための代表的な構造として以下の構造があります。

構造パターン	概要
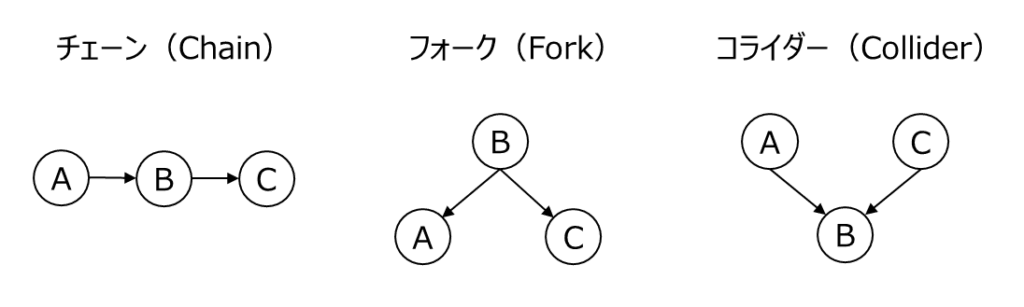
チェーン（Chain）	A → B → C のように、各変数が順に影響を与えるような構造です。
フォーク（Fork）	A ← B → C のように、1 つの変数 (B) が二つの変数 (A, C) に影響を与える構造です。
コライダー（Collider）	A → B ← C のように、2 つの変数 (A, C) が 1 つの変数 (B) に影響を与える構造です。

これらの構造の詳細や因果推論おける特徴については「チェーン、フォーク、コライダーの構造と特徴」を参考にしてください。まずは、因果推論で重要な構造パターンとして「チェーン」「フォーク」「コライダー」があることを理解しておいてください。

グラフの表現方法

グラフは、コンピューター上で扱いやすいように表現することが多いです。ここでは、代表的な隣接行列と GML（Graph Modelling Language）の 2 つの方法について説明します。また、Python でグラフのデータ構造やアルゴリズムを扱うためのライブラリである NetworkX を使った実例も紹介します。

隣接行列

隣接行列は、グラフを行列形式で表現する方法です。ノードが n 個ある場合には、n × n の行列を用意し、行列の (i, j) 要素が 1 である場合には、ノード i からノード j へのエッジがあることを示しています。

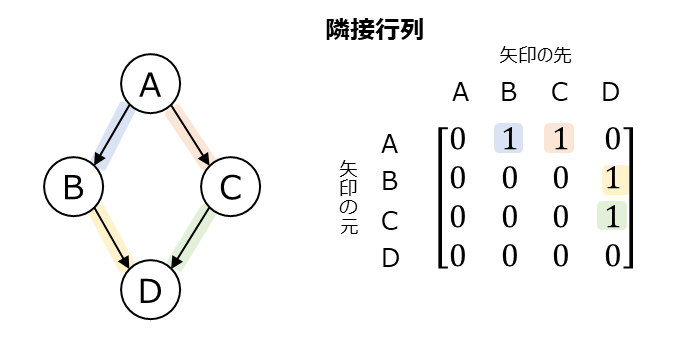
上記の隣接行列は、A → B、A → C、B → D、C → D といったエッジが存在する有向非巡回グラフの例です。

Pythonでの実装例

隣接行列を使った場合の Python におけるグラフ実装を見てみましょう。

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

# 隣接行列でグラフを表現する
adj_mat = np.array(
    [
        [0, 1, 1, 0],
        [0, 0, 0, 1],
        [0, 0, 0, 1],
        [0, 0, 0, 0],
    ]
)

# 隣接行列からグラフを構築する
graph = nx.DiGraph(adj_mat)

# ノードにラベルを割り当てる
mapping = {0: "A", 1: "B", 2: "C", 3: "D"}
graph = nx.relabel_nodes(graph, mapping)

# 可視化のためのレイアウトを指定
pos = nx.spring_layout(graph, seed=42)

# ノードとエッジを描画する
nx.draw(
    graph,
    pos,
    with_labels=True,
    node_color="skyblue",
    node_size=1000,
    edge_color="gray",
    arrowsize=20,
)

# グラフを描画する
plt.show()

上記例では、隣接行列は NumPy の ndarray を使用して配列として表現しています。配列を用意したら NetworkX パッケージの DiGraph に作成した行列を渡すことでグラフを簡単に作成できます。なお、無向グラフの場合は nx.Graph を使用します。

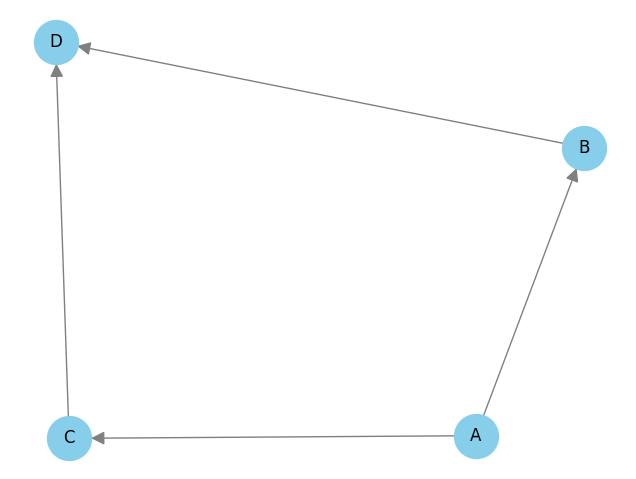
デフォルトではノードに 0 からの数字が割り当てられるので、A ～ D に変更する mapping を作成し、relabel_nodes を使ってラベルを変更しています。今回は NetworkX で用意されている spring_layout と Matplotlib を使用して描画しています。細かな描画設定の詳細は省略しますが、以下のようなグラフが生成できます。

GML（Graph Modeling Language）

GML（Graph Modelling Language）は、グラフをテキスト形式で記述するためによく使用されるフォーマットでグラフを扱うパッケージでよく利用されています。

graph [
  directed 1
  node [
    id 0
    label "A"
  ]
  node [
    id 1
    label "B"
  ]
  node [
    id 2
    label "C"
  ]
  node [
    id 3
    label "D"
  ]
  edge [
    source 0
    target 1
  ]
  edge [
    source 0
    target 2
  ]
  edge [
    source 1
    target 3
  ]
  edge [
    source 2
    target 3
  ]
]

上記において、directed 1 の場合は、有向グラフであることを示します。0 の場合は、無向グラフとなります。node がグラフにおけるノード（頂点）を、edge がグラフにおけるエッジ（辺）を示しています。

node を定義する際には、識別するための id と label を定義します。edge の定義でノード間をつなぐ場合には、source に矢印の元のノードの id を、target に矢印の先のノード id を指定します。

Pythonでの実装例

GML を使った場合の Python におけるグラフ実装を見てみましょう。

import matplotlib.pyplot as plt
import networkx as nx

# GMLでグラフを表現する
gml_sample = """graph [
  directed 1
  node [
    id 0
    label "A"
  ]
  node [
    id 1
    label "B"
  ]
  node [
    id 2
    label "C"
  ]
  node [
    id 3
    label "D"
  ]
  edge [
    source 0
    target 1
  ]
  edge [
    source 0
    target 2
  ]
  edge [
    source 1
    target 3
  ]
  edge [
    source 2
    target 3
  ]
]
"""

# GMLをパースしてグラフを構築する
graph = nx.parse_gml(gml_sample)

# ノードにラベルを割り当てる
mapping = {0: "A", 1: "B", 2: "C", 3: "D"}
graph = nx.relabel_nodes(graph, mapping)

# 可視化のためのレイアウトを指定
pos = nx.spring_layout(graph, seed=42)

# ノードとエッジを描画する
nx.draw(
    graph,
    pos,
    with_labels=True,
    node_color="skyblue",
    node_size=1000,
    edge_color="gray",
    arrowsize=20,
)

# グラフを描画する
plt.show()

GML でグラフを表現した文字列を gml_sample で用意しています。GML を解釈してグラフを構築するには NetworkX の parse_gml を使うことで簡単に実現できます。

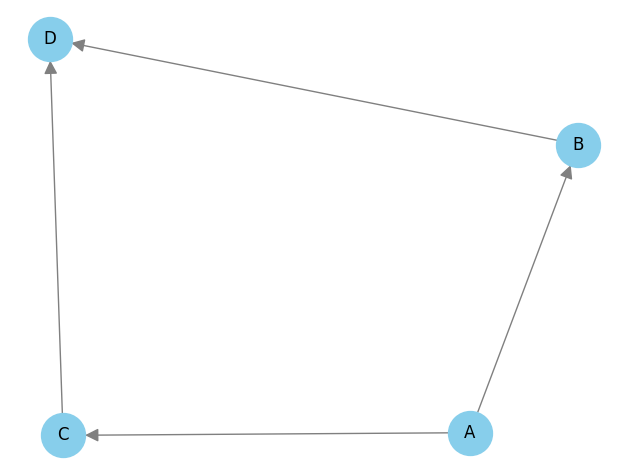
以降の可視化の部分は隣接行列の場合と同様でグラフを可視化することが可能です。