確率的グラフィカルモデルの重要な概念であるd分離（d-separation）について解説します。d分離は、グラフ構造に関する概念ですが因果推論などでも重要な概念になります。
Contents
d分離（d-separation）とは？
d分離の概要
因果推論では、変数間の関係を因果ダイアグラム（Causal Diagram）、特に有効非巡回グラフ（DAG: Directed Acyclic Graph）を用いて表現することが一般的です。因果ダイアグラムについては「因果ダイアグラムの概要」でまとめているので参考にしてください。
グラフにおけるd分離（d-separation）とは、2つのノード（変数）の集合XとYの間の統計的依存関係が遮断されることを意味します。つまり、d分離が成り立つとき、適切な確率分布のもとでXとYは独立となります。ただし、全ての確率分布で成り立つわけではなく、特にベイジアンネットワークの仮定（DAGに沿った因果構造をもつ確率分布）では、d分離であれば統計的独立が保証されます。
なお、d分離は因果推論に特化した概念ではなく、グラフィカルモデル全般において使用される統計的独立性の判断基準です。例えば、ベイジアンネットワークや機械学習における確率的モデリングの分野でも重要な役割を果たします。
因果推論の分野では、d分離を用いることで観測データに基づく推論の際に、どの変数をコントロールするべきか判断するのに役立ちます。この記事では、d分離の概要について紹介します。
d分離の定式化
d分離の説明していくにあたってまずは一般的な考え方として表現してみます。
ノードの集合としてX、Y、Zがあるとします。より簡単にはノード1つで考えることですが、集合の要素が1つである場合と思ってもらえればよいです。このとき、XとYを結ぶすべてのパスがZによってブロックされているときXとYはZによってd分離されていると言います。
例えば、例として以下のようなグラフが考えられます。上部の図は複数のノードから成り立っていますが、集合X、YとZに分類することができます。下部の図は各集合一つのノードだった場合の例です。
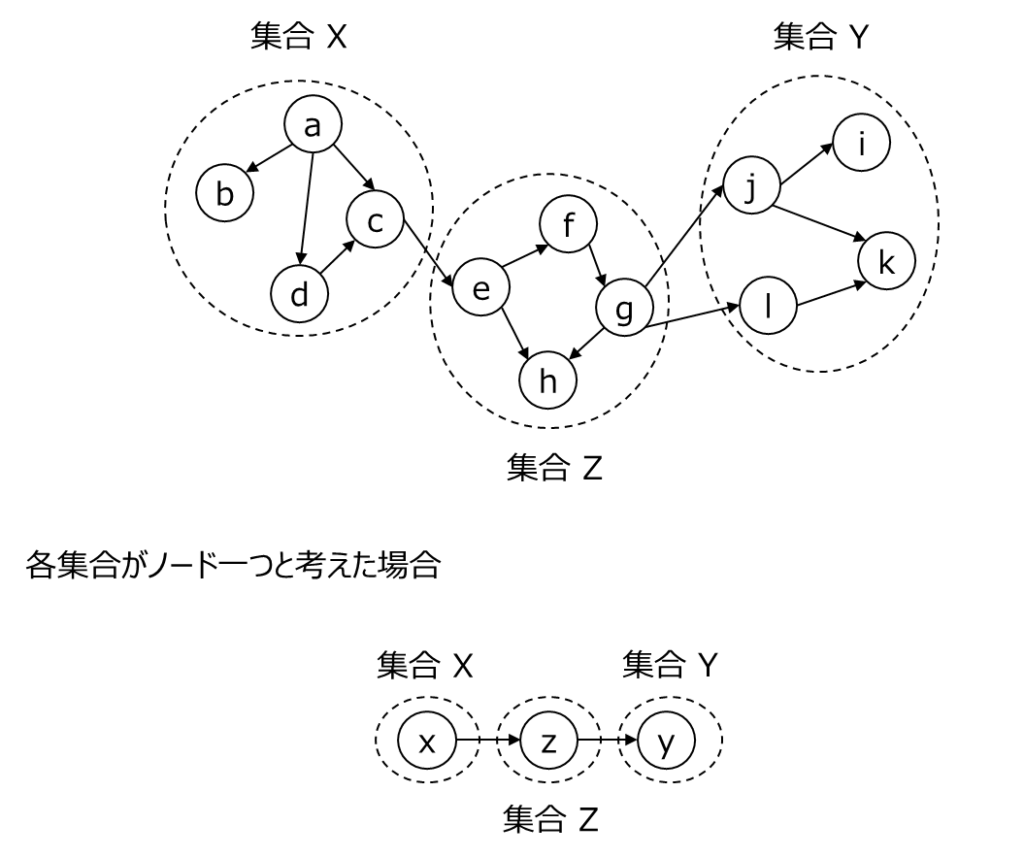
これらのグラフが与えられたときにパスがブロックされてd分離されるかの判断基準について以降で説明していきます。
チェーン、フォーク、コライダーとの関連性
因果推論の因果ダイアグラムにおいて重要な構造としてチェーン、フォーク、コライダーという構造があります。これらの構造については「チェーン、フォーク、コライダーの構造と特徴」で個別に取り上げているので参考にしてください。
これらの重要な構造とd分離の関係については以下のように整理できます。XとYの関係性においてZに条件付けるかどうかでd分離（パスがブロック）されるかが判断できるわけです。
| 構造 | 構造 | 関係性 |
|---|---|---|
| チェーン構造 | X → Z → Y | [Zに条件付けない場合] XからYへのパスは開いており、XとYはZを介して関連を持つ可能性があります。Zは媒介因子と呼ばれます。 [Zに条件付ける場合] XとYのパスは閉じ、XとYは条件付き独立（d分離）となります。 |
| フォーク構造 | X ← Z → Y | [Zに条件付けない場合] XとYはZを介して関連を持つ可能性があります。Zは交絡因子と呼ばれ、ZによってXとYに相関が生じることがあります。 [Zに条件付ける場合] XとYの間の依存関係が取り除かれて、条件付き独立（d分離）となります。 |
| コライダー構造 | X → Z ← Y | [Zに条件付けない場合] XとYは統計的に独立（d分離）しています。 [Zに条件付ける場合] Zに条件付けると、XとYの間に見せかけの相関が生じます。これをコライダー・バイアスと言います。 |
【補足】「条件付ける」と「コントロールする」の違い
因果推論の勉強をしていると「条件付ける」という言葉や「コントロールする」という言葉が出てきます。これらについては、使われ方によってほぼ同じ意味で使われることがありますが、厳密にはニュアンスが少し異なります。
条件付ける（Conditioning）
「条件付ける」という言葉は、統計的な意味合いが強い場合で使用されます。確率分布の条件を設定することを指していて条件付確率 P(X,Y|Z)のように表されます。
あるノード（変数）の情報を得ることにより確率分布が変わるイメージです。例えば、ある病気の診断Zを知ったうえで、遺伝子Xと生活習慣Yの関係を考えるような場合、Zに条件付けると言います。
コントロール（Controlling）
「コントロールする」という言葉は、因果推論の文脈で使われることが多いです。「ある変数の影響を取り除く」ことを意図します。
実際のデータ分析では、回帰モデルの説明変数として対象変数を入れることをコントロールすると表現します。例えば、年収Zをコントロール(年収帯を固定するなど)することで、教育水準Xと健康状態Yの関係性を見極めるような場合です。
どのように使うべきか
まとめてみると「条件付ける」と「コントロールする」という表現は以下のように使い分けることが適切であると言えます。
- d分離の文脈：「条件付ける」という表現が適切
- 因果推論の文脈：「コントロールする」という表現が適切
まとめ
確率的グラフィカルモデルの重要な概念であるd分離（d-separation）について解説しました。d分離は因果推論に特化した概念ではなく、グラフィカルモデル全般において使用される統計的独立性の判断基準ですが、この記事では因果推論に絡めつつ説明をしました。
d分離を判断するためには、チェーン、フォーク、コライダーといったグラフにおける重要な構造に紐づけて調べる必要があります。d分離を用いることで観測データに基づく推論の際に、どの変数をコントロールするべきか判断するのに役立ちますので、d分離についてぜひ学んでみてください。
