NumPyの特徴的な機能であるブロードキャスト（broadcast）の基本的な考え方を紹介します。
Contents
ブロードキャスト（broadcast）の基本
NumPyの特徴的な機能としてブロードキャスト（broadcast）という機能があります。ブロードキャストは、NumPyが高速にベクトル演算するユニバーサル関数（ufunc）の土台となる機能です。
ユニバーサル関数（ufunc）については以下で概要をまとめているので参考にしてみてください。
ブロードキャスト（broadcast）の基本的な考え方
ブロードキャストの基本的な考え方について、簡単な例を使いつつ見ていきましょう。
ユニバーサル関数のベクトル計算
まずは、ユニバーサル関数（ufunc）のベクトル計算のイメージから見ていきます。以下は同じサイズのNumPyの配列（ndarray）を足し算するプログラムの例です。
import numpy as np
x1 = np.arange(1, 6)
print(f'x1 = {x1}')
x2 = np.arange(6, 11)
print(f'x2 = {x2}')
print(f'x1 + x2 = {x1 + x2}')
【実行結果】 x1 = [1 2 3 4 5] x2 = [ 6 7 8 9 10] x1 + x2 = [ 7 9 11 13 15]
ユニバーサル関数では、ベクトル演算をしますので各要素ごとの演算が行われます。イメージ図にしてみると以下のようになります。
今回は足し算（+）の例ですが、他の演算でも考え方は同様です。
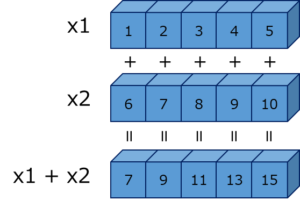
ブロードキャスト例（1次元）
上記で見た例は、配列の形状が一致している場合の例でした。では配列の形状（shape）が異なる場合はどうなるでしょうか。
以下は配列と数値の足し算をしてみているプログラム例です。このような場合にブロードキャストの機能が動作します。
import numpy as np
x1 = np.arange(1, 6)
print(f'x1 = {x1}')
print(f'x1 + 5 = {x1 + 5}')
【実行結果】 x1 = [1 2 3 4 5] x1 + 5 = [ 6 7 8 9 10]
上記結果を見ると、x1の各要素にそれぞれ5が足し算されていることが分かります。この時、NumPyは5という数字を拡張して、x1と同じ形状になる配列にしてからベクトル計算をしています。
イメージ図にしてみると以下のようになります。
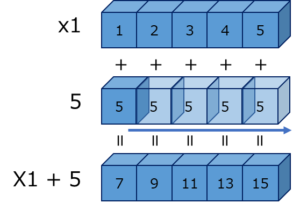
ブロードキャスト例（2次元：行方向）
次に2次元配列の場合も見てみましょう。
以下の例はnp.eyeで5×5の単位行列を作成しています。足し算するのは、1次元の1~5までの数字が入った配列です。
import numpy as np
x1 = np.eye(5)
print(f'x1 = \n{x1}')
x2 = np.arange(1, 6)
print(f'x2 = {x2}')
print(f'x1 + x2 = \n{x1 + x2}')
【実行結果】 x1 = [[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]] x2 = [1 2 3 4 5] x1 + x2 = [[2. 2. 3. 4. 5.] [1. 3. 3. 4. 5.] [1. 2. 4. 4. 5.] [1. 2. 3. 5. 5.] [1. 2. 3. 4. 6.]]
上記の例では、行方向のサイズが異なっているので、x2の配列を行方向に拡張して、x1と同じ形状にして計算がされます。
イメージ図としては以下のようになります。
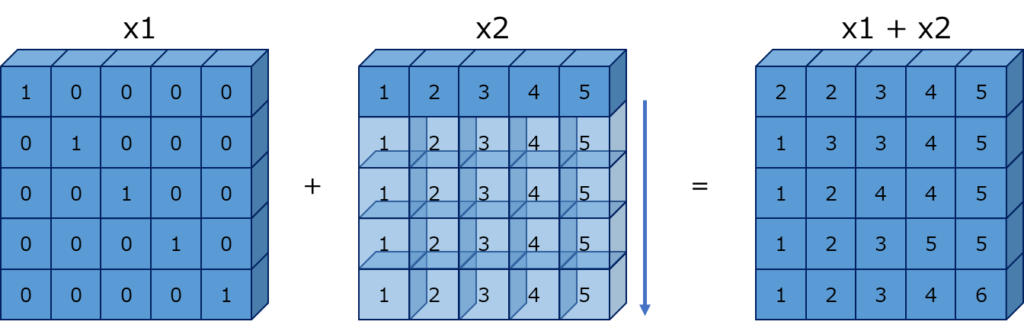
ブロードキャスト例（2次元：列方向）
次に列方向に拡張される例も見てみましょう。
import numpy as np
x1 = np.eye(5)
print(f'x1 = \n{x1}')
x2 = np.arange(1, 6)[:, np.newaxis]
print(f'x2 = {x2}')
print(f'x1 + x2 = \n{x1 + x2}')
【実行結果】 x1 = [[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]] x2 = [[1] [2] [3] [4] [5]] x1 + x2 = [[2. 1. 1. 1. 1.] [2. 3. 2. 2. 2.] [3. 3. 4. 3. 3.] [4. 4. 4. 5. 4.] [5. 5. 5. 5. 6.]]
上記の例では、列方向のサイズが異なっているので、x2の配列を列方向に拡張して、x1と同じ形状にして計算がされます。
イメージ図としては以下のようになります。
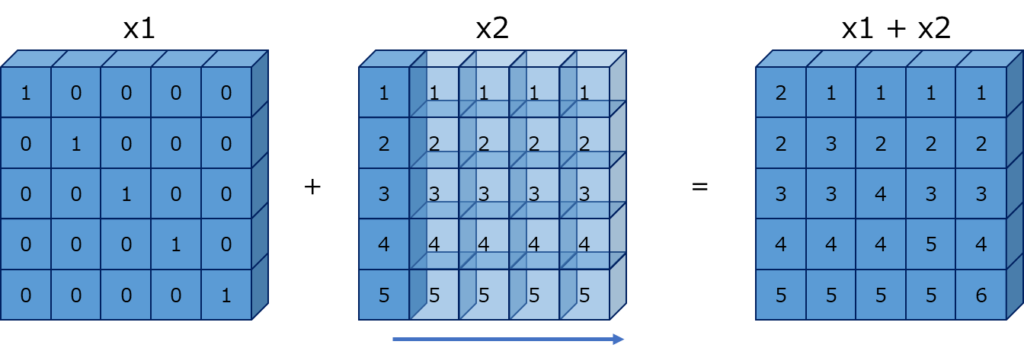
ブロードキャスト（broadcast）のルール
これまで見てきた例は非常にシンプルな例です。もっと詳細なブロードキャストの具体的なルール等に興味がある方は、公式ドキュメントのGeneral Broadcasting Rulesというところに記載がありますので、そちらを参照してください。
NumPyのユニバーサル関数（ufunc）ではブロードキャストという機能が動いて形状（shape）が揃えられているということを意識してみるとよいでしょう。
ブロードキャストの公式ドキュメントの記載はこちらを参照してください。
