【Python】集合（set）の演算（積集合・和集合・差集合・排他的論理和）と包含関係の判定（上位集合・部分集合）

Python の集合（set） の演算と集合の包含関係の判定方法について解説します。

集合（set）の演算と包含関係の判定

集合（set）とは、プログラミングで用いられるデータの型の 1 種で、順序のないデータの集まりです。同一のデータは集合には 1 つしかないようなデータとなります。Python でも、集合は set として用意されています。

集合の演算としては積集合、和集合、差集合、排他的論理和があります。また、集合間の包含関係として、上位集合、部分集合の判定が必要な場合があります。

この記事では、演算（積集合・和集合・差集合・排他的論理和）の計算方法と集合の包含関係（上位集合・部分集合）の判定方法について説明します。

集合（set）の演算

積集合

積集合は、集合が重なっている部分のことを言います。図で表すと以下で色を塗った部分になります。

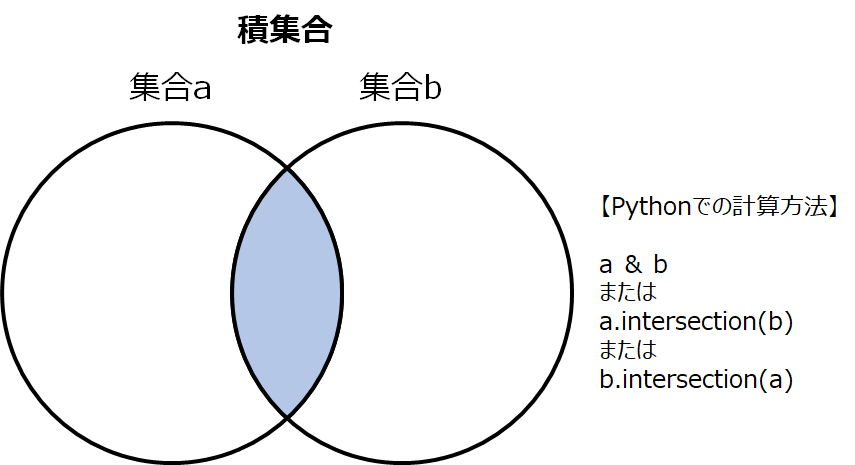
積集合を計算するには、& 演算子 か intersection を使用します。

a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

# 積集合の計算
print(f"a & b: {a & b}")
print(f"a.intersection(b): {a.intersection(b)}")
print(f"b & a: {b & a}")
print(f"b.intersection(a): {b.intersection(a)}")

【実行結果】
a & b: {6, 7, 8, 9, 10}
a.intersection(b): {6, 7, 8, 9, 10}
b & a: {6, 7, 8, 9, 10}
b.intersection(a): {6, 7, 8, 9, 10}

結果を見てみると a と b で重なっているデータが抽出できています。なお、積集合は a を基準に実行しても、b を基準に実行しても結果は同じです。

今回は数値サンプルですが、例えば名前の集合など文字列の集合についても同じです。

和集合

和集合は、いずれの集合も含む全体部分のことを言います。図で表すと以下で色を塗った部分になります。

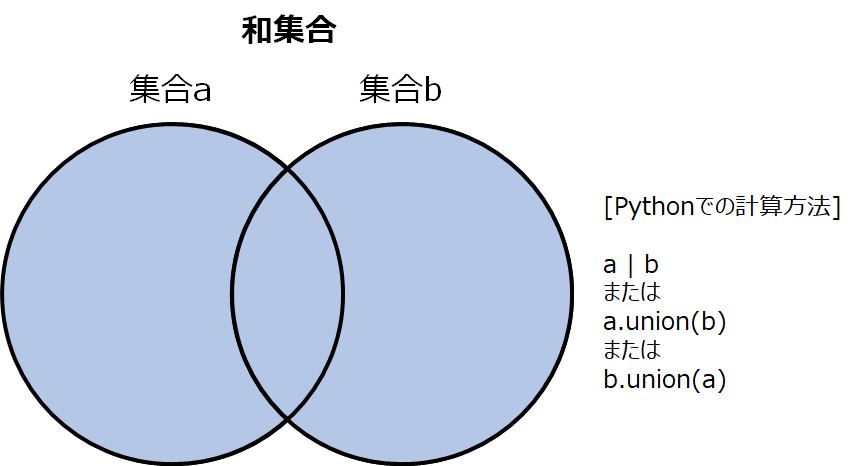
和集合を計算するには、| 演算子 か union を使用します。

a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

# 和集合の計算
print(f'a | b: {a | b}')
print(f'a.union(b): {a.union(b)}')
print(f"b | a: {b | a}")
print(f'b.union(a): {b.union(a)}')

【実行結果】
a | b: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
a.union(b): {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
b | a: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
b.union(a): {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

結果を見てみると a と b に含むデータ全体が抽出できています。なお、和集合は a を基準に実行しても、b を基準に実行しても結果は同じです。

差集合

差集合は、片方の集合からもう片方の集合に含まれる要素を取り除いた部分のことを言います。図で表すと以下で色を塗った部分になります。

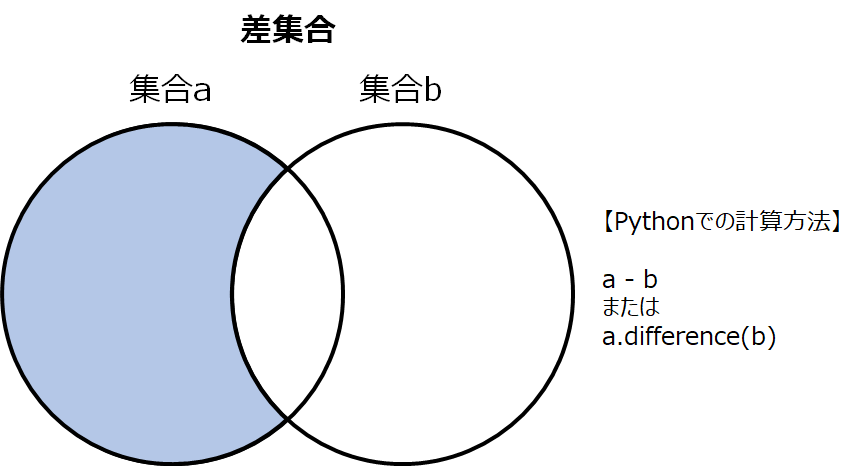
差集合を計算するには、- 演算子 か difference を使用します。

a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

# 差集合の計算
print(f"a - b: {a - b}")
print(f"a.difference(b): {a.difference(b)}")
print(f"b - a: {b - a}")
print(f"b.difference(a): {b.difference(a)}")

【実行結果】
a - b: {1, 2, 3, 4, 5}
a.difference(b): {1, 2, 3, 4, 5}
b - a: {11, 12, 13, 14, 15}
b.difference(a): {11, 12, 13, 14, 15}

結果を見てみると a と b の差のデータが抽出できています。差集合については、a を基準にする (a-b) か、b を基準にする (b-a) かで結果が変わるので注意しましょう。

排他的論理和

排他的論理和は、両方の集合の領域から集合が重なる部分を除いた部分のことを言います。図で表すと以下で色を塗った部分になります。

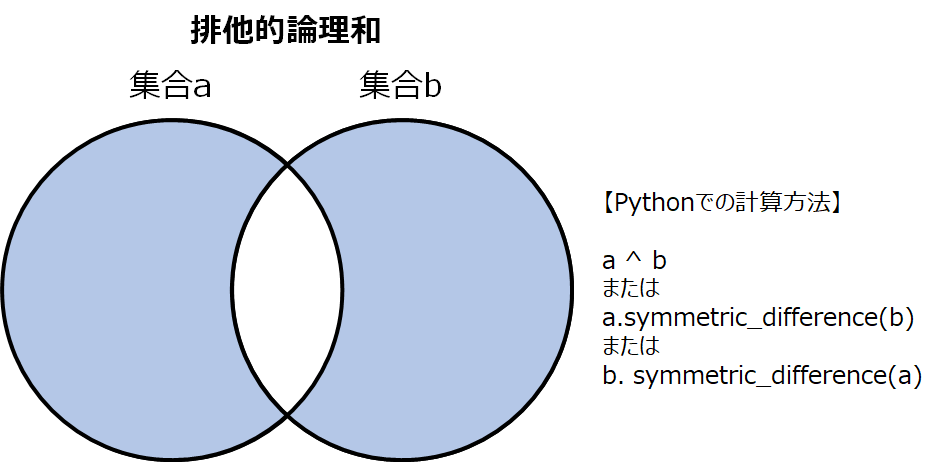
排他的論理和を計算するには、^ 演算子 か symmetric_difference を使用します。

a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

# 排他的論理和の計算
print(f'a ^ b: {a ^ b}')
print(f'a.symmetric_difference(b): {a.symmetric_difference(b)}')
print(f'b ^ a: {b ^ a}')
print(f'b.symmetric_difference(a): {b.symmetric_difference(a)}')

【実行結果】
a ^ b: {1, 2, 3, 4, 5, 11, 12, 13, 14, 15}
a.symmetric_difference(b): {1, 2, 3, 4, 5, 11, 12, 13, 14, 15}
b ^ a: {1, 2, 3, 4, 5, 11, 12, 13, 14, 15}
b.symmetric_difference(a): {1, 2, 3, 4, 5, 11, 12, 13, 14, 15}

結果を見てみると a と b を足した部分から、重なっている部分を除いたデータが抽出できています。なお、排他的論理和は a を基準に実行しても、b を基準に実行しても結果は同じです。

集合（set）の包含関係の判定方法

集合を扱うときには、集合の包含関係を調べたくなることがあります。図を使いつつ包含関係に関する用語をまず整理し、Python での判定方法を見ていきましょう。

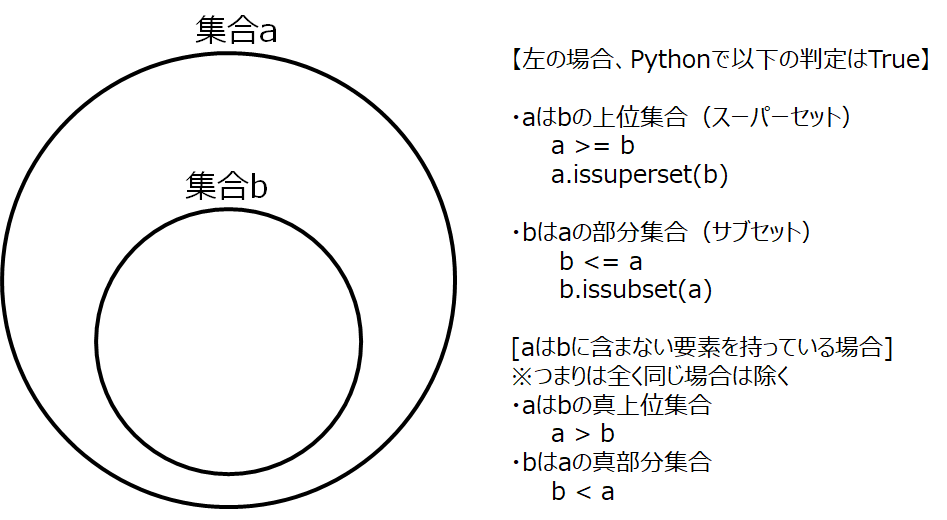
上記の図で、集合 a は集合 b に含む要素をすべて持っています。この時、a は b の上位集合（スーパーセット）と言います。一方で、b は a の部分集合（サブセット）と言います。

また、a は b に含まない要素を持っている場合（つまり、全く同じ集合でない場合）は、a は b の真上位集合、b は a の真部分集合といいます。

集合が等しいかどうかの判定

集合が等しいことを判定する場合は、== 演算子を、集合が等しくないことを判定する場合は、!= 演算子を使用します。結果は True、False で判断できます。

# aとbは等しい
a = {1, 2, 3, 4, 5}
b = {1, 2, 3, 4, 5}

print("===== aとbが等しい場合")
print(f"a == b: {a == b}")
print(f"a != b: {a != b}")

# aとbは等しくない
a = {1, 2, 3, 4, 5}
b = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

print("===== aとbが等しくない場合")
print(f"a == b: {a == b}")
print(f"a != b: {a != b}")

【実行結果】
===== aとbが等しい場合
a == b: True
a != b: False
===== aとbが等しくない場合
a == b: False
a != b: True

上位集合と真上位集合

上位集合を判定する場合には、>= 演算子 か issuperset メソッドを使用します。また、真上位集合かを判定する場合は、> 演算子を使用します。結果は True、False で判断できます。

# aはbの真上位集合
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {1, 2, 3, 4, 5}

print("===== aはbの真上位集合である場合")
print(f"a >= b: {a >= b}")
print(f"a.issuperset(b): {a.issuperset(b)}")
print(f"a > b: {a > b}")

# aはbの上位集合であるが、真上位集合ではない
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

print("===== aはbの上位集合であるが、真上位集合ではない場合")
print(f"a >= b: {a >= b}")
print(f"a.issuperset(b): {a.issuperset(b)}")
print(f"a > b: {a > b}")

【実行結果】
===== aはbの真上位集合である場合
a >= b: True
a.issuperset(b): True
a > b: True
===== aはbの上位集合であるが、真上位集合ではない場合
a >= b: True
a.issuperset(b): True
a > b: False

部分集合と真部分集合

部分集合を判定する場合には、<= 演算子 か issubset メソッドを使用します。また、真部分集合かを判定する場合は、< 演算を使用します。結果は True、False で判断できます。

# bはaの真部分集合
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {1, 2, 3, 4, 5}

print("===== bはaの真部分集合である場合")
print(f"b <= a: {b <= a}")
print(f"b.issubset(a): {b.issubset(a)}")
print(f"b < a: {b < a}")

# bはaの部分集合であるが、真部分集合ではない
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

print("===== bはaの部分集合であるが、真部分集合ではない場合")
print(f"b <= a: {b <= a}")
print(f"b.issubset(a): {b.issubset(a)}")
print(f"b < a: {b < a}")

【実行結果】
===== bはaの真部分集合である場合
b <= a: True
b.issubset(a): True
b < a: True
===== bはaの部分集合であるが、真部分集合ではない場合
b <= a: True
b.issubset(a): True
b < a: False

まとめ

Python の集合（set） の演算と集合の包含関係の判定方法について解説しました。

集合の演算としては、積集合、和集合、差集合、排他的論理和の計算方法を紹介しています。また、集合の包含関係として、上位集合か部分集合かを判断する方法についても説明しています。

各メソッドの使い方をしっかりと理解して、適切に計算できるようになってもらえたらと思います。

あわせて読みたい

【Python Tech】プログラミングガイド

ホッシー

システムエンジニア

Contact

はじめまして。当サイトをご覧いただきありがとうございます。 私は製造業のメーカーで、DX推進や業務システムの設計・開発・導入を担当しているシステムエンジニアです。これまでに転職も経験しており、以前は大手電機メーカーでシステム開発に携わっていました。

プログラミング言語はこれまでC、C++、JAVA等を扱ってきましたが、最近では特に機械学習等の分析でも注目されているPythonについてとても興味をもって取り組んでいます。これまでの経験をもとに、Pythonに興味を持つ方のお役に立てるような情報を発信していきたいと思います。どうぞよろしくお願いいたします。

※キャラクターデザイン：ゼイルン様