【scikit-learn】KMeansでk-means法によるクラスタリングをする方法

Pythonの機械学習ライブラリであるsciki-learnのKMeansを使ってk-means法によるクラスタリングを行う方法を解説します。

k-means法によるクラスタリング

k-means法とは、教師なし学習で代表的なクラスタリングの中でも有名な手法の一つです。分類アルゴリズムのk-近傍法とは異なるため注意しましょう。k-近傍法については「k近傍法（k-NN）を用いたデータ分類方法」で紹介していますのでもし興味あれば参考にしてください。

k-means法のアルゴリズムの手順概要を説明すると以下のようになります。

1. データの中からk個のデータ点を任意に抽出して、初期値のセントロイドとして設定する。その後に、以下の2, 3のステップを反復する。
2. 全てのデータ点を最も近いセントロイドにそれぞれ割り振る。
3. 各k個のセントロイドに割り振られたデータの重心を計算して、その重心を新しいセントロイドとして更新する。

ここでセントロイドと言っているのは、各クラスタの中心の事です。

k-means法では、SSE（Sum of Squared Errors）というクラスタ内の誤差平方和を用いて、このSSEを最小化するようにセントロイドが選ばれていきます。また、k-means法は、クラスタ数を事前に指定しないとクラスタリングできないことも特徴です。

k-means法によるクラスタリングは、Pythonの機械学習ライブラリであるscikit-learnにてKMeansとして実装がされています。

本記事では、scikit-learnのKMeansを使ったクラスタリング方法の実装例を紹介します。また、クラスタ数を決める方法の一つであるエルボー法についても解説します。

scikit-learnのKMeansを使ったk-means法によるクラスタリング方法

k-menas法の使い方（sklearn.cluster.KMeans）

実装例

scikit-learnのmake_blogsでクラスタリング用のデータを用意し、KMeansを使ってk-means法によるクラスタリングする方法について紹介します。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans


def main():
    """メイン関数"""
    np.random.seed(1)

    # ===== データの生成
    k = 5
    data, label = make_blobs(n_samples=500, n_features=2, centers=k, cluster_std=1.0)

    # ===== k-meansクラスタリング
    km = KMeans(n_clusters=k)
    pred = km.fit_predict(data)

    # ===== SSE値を出力
    print(f"SSE: {km.inertia_:.2f}")

    # ===== クラスタリング結果を描画する
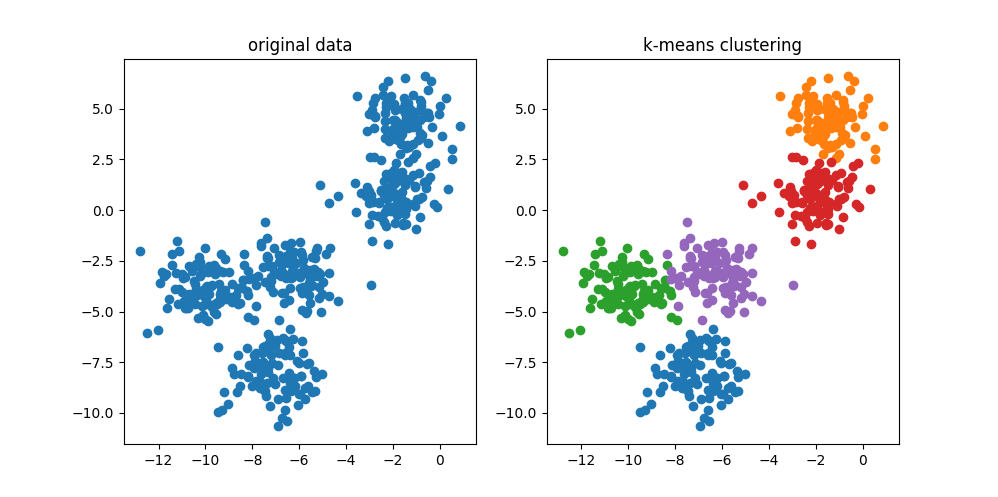
    fig, ax = plt.subplots(1, 2, figsize=(10, 5))
    # 元データを表示する
    ax[0].scatter(data[:, 0], data[:, 1])
    ax[0].set_title("original data")
    # クラスタリング結果を表示する
    for i in range(k):
        ax[1].scatter(data[pred == i, 0], data[pred == i, 1])
    ax[1].set_title("k-means clustering")
    plt.show()


if __name__ == "__main__":
    main()

【実行結果】
SSE: 894.48

実装内容の解説

上記で紹介して実装例の各部分ごとに内容を解説していきます。

必要モジュールのインポート

from sklearn.cluster import KMeans

k-meansクラスタリングを使用するには、sklearn.clusterからKMeansをインポートします。他にもnumpy等インポートしていますがそちらの説明は省略します。

データセットの準備

    np.random.seed(1)

    # ===== データの生成
    k = 5
    data, label = make_blobs(n_samples=500, n_features=2, centers=k, cluster_std=1.0)

データは、make_blobsを使用して生成します。引数として指定しているのは以下のような項目です。

• n_sample：データの点数
• n_features：データの次元数
• centers：クラスタの数
• cluster_std：各クラスタの標準偏差

今回は、5つのクラスタを作成しています。また、教師なし学習のため、labelの方は使用していません。乱数シードは、np.random.seedで設定していますが、make_blobsのrandom_state引数で指定することも可能です。

k-meansクラスタリングの実行

    # ===== k-meansクラスタリング
    km = KMeans(n_clusters=k)
    pred = km.fit_predict(data)

上記の部分でk-meansクラスタリングを実行しています。n_clustersでクラスタ数を指定します。クラスタリングはfit_predictメソッドを使うことで実行することができます。

SSE（誤差平方和）の取得

    # ===== SSE値を出力
    print(f"SSE: {km.inertia_:.2f}")

計算されたSSE（誤差平方和）については、inertia_を参照することで取得することができます。

クラスタリング結果の表示

    # ===== クラスタリング結果を描画する
    fig, ax = plt.subplots(1, 2, figsize=(10, 5))
    # 元データを表示する
    ax[0].scatter(data[:, 0], data[:, 1])
    ax[0].set_title("original data")
    # クラスタリング結果を表示する
    for i in range(k):
        ax[1].scatter(data[pred == i, 0], data[pred == i, 1])
    ax[1].set_title("k-means clustering")
    plt.show()

上記の部分は、元データとクラスタリング結果を横に並べて表示している部分です。

結果の図を再掲しますが、5クラスのデータに分類できていることが分かるかと思います。

エルボー法によるクラスタ数の決定

k-means法によるクラスタリングでは、実行前にクラスタ数を決めて指定する必要があります。上記の例では、方法の説明のために分かりやすいように5つのクラスタのデータセットを作り、そのデータセットに対してk=5でk-meansクラスタリングを実行したため、きれいにクラスタリングができていました。

しかし、実際の適用場面では、データがいくつのクラスタになるかは事前に分かりません。では、kの数をどう決めればよいでしょうか。

クラスタ数を決めるときに参考になる手法としてエルボー法という方法があります。エルボー法では、k-meansに指定するクラスタ数の数を増やしていったときにSSEがどのように変化するかをプロットし、その結果からクラスタ数を決定する方法です。

クラスタ数を増やしていってSSEをプロットするとグラフが、かくっと曲がって変化が少なくなる部分が出てきます。エルボー法では、この時のクラスタ数を最適とします。なぜ「エルボー」というかというと、SSEのプロット形状が肘が曲がっているように見えることからだそうです。

では、エルボー法でクラスタ数を調べてみるサンプルプログラムを見てみましょう。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans


def main():
    """メイン関数"""
    np.random.seed(1)

    # ===== データの生成
    k = 5
    data, label = make_blobs(n_samples=500, n_features=2, centers=k, cluster_std=1.0)

    # ===== エルボー法
    sse = []
    for k in range(1, 11):
        km = KMeans(n_clusters=k)
        km.fit(data)
        sse.append(km.inertia_)

    # ===== SSE値をプロットする
    plt.plot(range(1, 11), sse, "o-")
    plt.title("elbow method")
    plt.xlabel("number of clusters")
    plt.ylabel("sse")
    plt.show()


if __name__ == "__main__":
    main()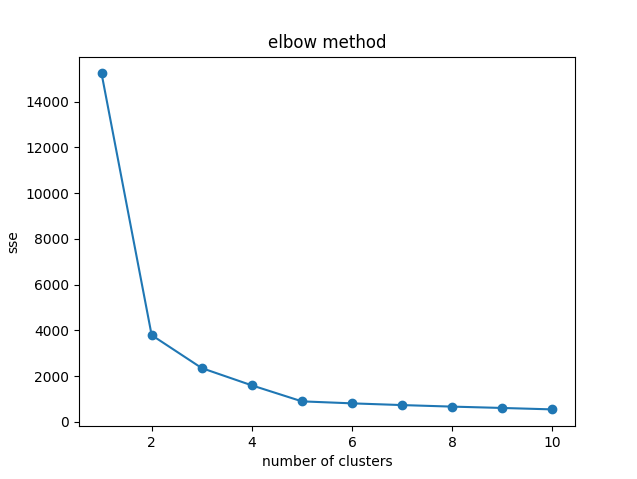

上記では、kを1~10まで変えつつ、KMeansを使ったk-meansクラスタリングを実行しています。そして、図は各kにおけるSSEの値をリストに蓄積してグラフにプロットしたものになります。

この結果を見るとクラスタ数が5のところまでは降下が大きいのに対して5以降については緩やかになっているように見えます。このため、kの適切な値は5ではないかと予想できます。これがエルボー法での考え方になります。

今回は、分かりやすい分類データを使っているのできれいなプロット図になっていますが、現実的な問題に対しては、正直これほどきれいには分からない場合が多いのではないかと思います。

まとめ

Pythonの機械学習ライブラリであるsciki-learnのKMeansを使ってk-means法によるクラスタリングを行う方法を解説してきました。また、k-meansにて指定するクラスタ数を決める一つの方法であるエルボー法についても簡単にご紹介しています。

k-means法は、教師なし学習で代表的なクラスタリングの中でも有名な手法の一つです。scikit-learnのKMeansの使い方も非常に簡単ですので、是非使い方を覚えてみてもらいたいと思います。

【Python Tech】プログラミングガイド本サイトで紹介しているPython入門、応用に関する記事のまとめページです。Python文法の入門から高度な内容、おすすめの書籍についても紹介しています。また、機械学習等のデータ分析やGUI開発、近年話題の生成AI等のトピックスについても含んでいます。...

ホッシー

システムエンジニア

Contact

はじめまして。当サイトをご覧いただきありがとうございます。 私は製造業のメーカーで、DX推進や業務システムの設計・開発・導入を担当しているシステムエンジニアです。これまでに転職も経験しており、以前は大手電機メーカーでシステム開発に携わっていました。

プログラミング言語はこれまでC、C++、JAVA等を扱ってきましたが、最近では特に機械学習等の分析でも注目されているPythonについてとても興味をもって取り組んでいます。これまでの経験をもとに、Pythonに興味を持つ方のお役に立てるような情報を発信していきたいと思います。どうぞよろしくお願いいたします。

※キャラクターデザイン：ゼイルン様