TensorFlow/Kerasを用いて、RNN（Recurrent Neural Network：リカレントニューラルネットワーク）による時系列データ予測をする方法について解説します。一つの例として、正弦波（Sin波）にノイズを載せたデータを使ってSin波を予測をする例を紹介します。
Contents
RNN（Recurrent Neural Network：リカレントニューラルネットワーク）
RNN（Recurrent Neural Network：リカレントニューラルネットワーク）とは、時系列データに対してディープラーニングを行う際に適したモデルのことを言います。
一般的な全結合のニューラルネットワークやCNN（Convolutional Neural Network：畳み込みニューラルネットワーク）では、データに関する記憶を持っていません。ここで記憶と言っているのは過去データのことであり、全結合ネットワークやCNNでは個々のデータが個別に処理されるため、入力をまたがって情報が保持されることはありません。
ただ、時系列データというのは前に現れたデータがその後のデータに何かしらの影響を与えていると考えられるため、時系列データをまとめて考える必要があります。RNNは、このような時系列データに適したモデルであると理解してもらえればよいと思います。
本記事では、RNNの概要を説明するとともにTensorFlow/KerasのSimpleRNNを用いたRNNによる時系列データ予測の実装例を紹介します。
RNNの構成概要
RNN（Recurrent Neural Network：リカレントニューラルネットワーク）は、よく以下のようなループ構造を持つネットワークとして表現されます。
ただ、再帰と書かれても私は最初いまいちよく分かりませんでした。RNNは以下のような表現をされる場合もありますが、私は以下の方がイメージがしやすいかなと思っています。
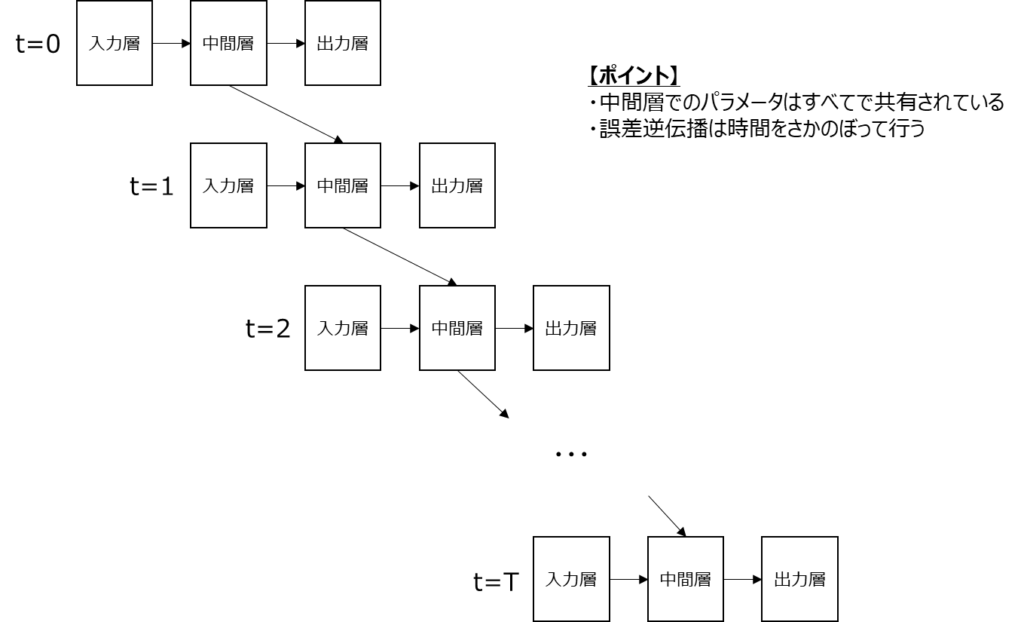
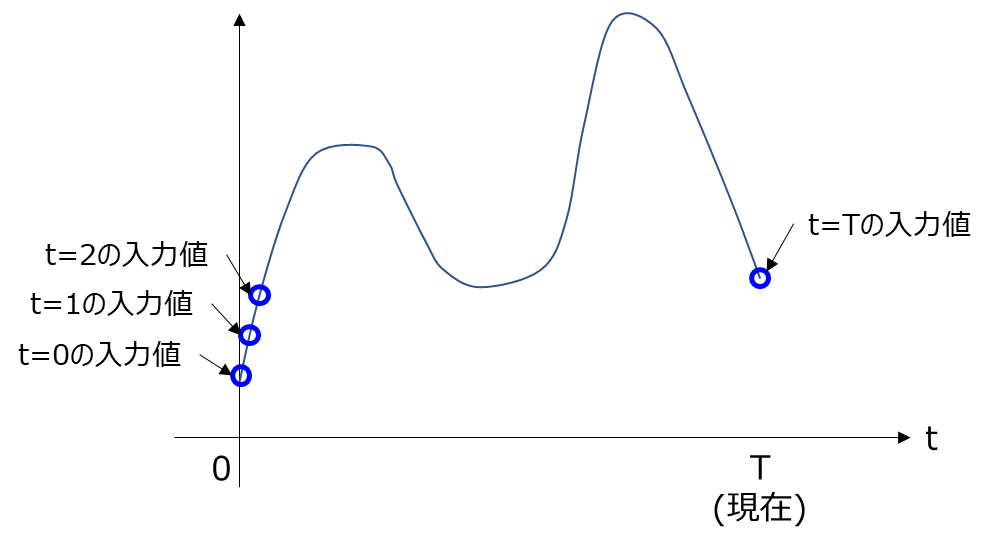
この図では、各時刻の入力を明確に分けて書いた図です。例えば、以下のようなある波形があったときには各時刻tにおける波形の値が入力各tの入力層への入力になります。
RNNとしてしっかりと理解しておかなければならないのは、中間層で持つパラメータ（重み）は各時刻で共有されているということです。また、誤差逆伝搬の際には、矢印で書かれている接続部分を逆に誤差がたどっていくということになります。
RNN出力層は、上記のように各時刻に対する出力を持つタイプと以下の図のように現時刻（以下例ではt=T）の出力のみ持つタイプがあります。どちらが良いということはなく、どちらが良いかはケースバイケースと言われています。ただ、現在時刻の出力は過去入力により決まるという考え方とすると、以下の図のモデルの方がしっくりとくる気もしています。
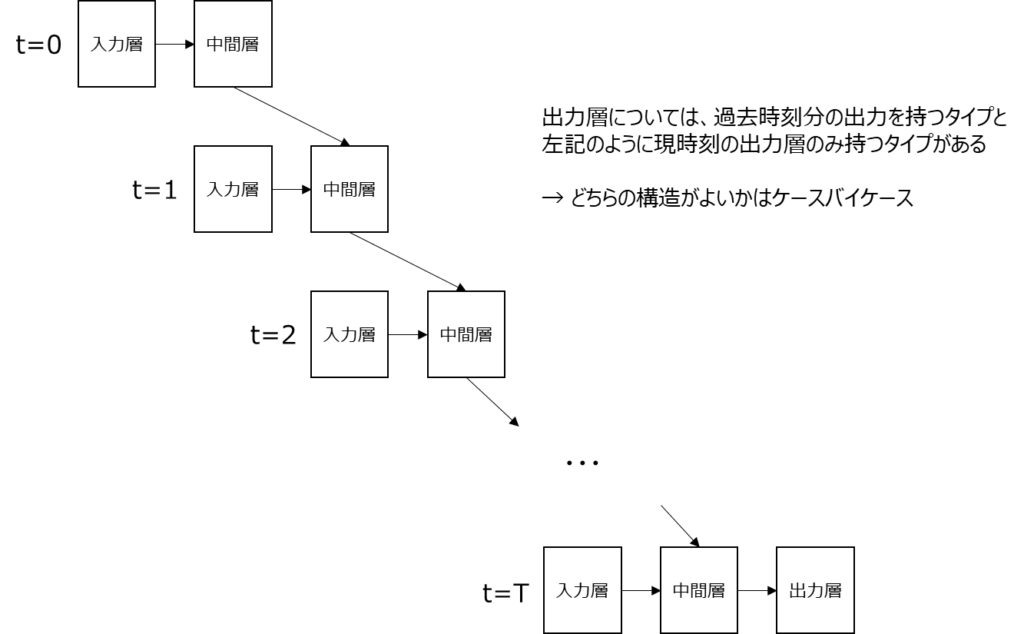
TensorFlow/Kerasを用いたRNNによる時系列データ予測の実装
以降では、TensorFlow/Kerasを用いたRNNによる時系列データの予測に関する実装例を紹介していきます。TensorFlow/Kerasでは、SimpleRNNと呼ばれる層が既に実装されています。このSimpleRNNの使い方を中心に説明をしていきます。
データとしては、簡単な例とするために正弦波（sin波）のデータをデータを用います。問題設定として、ある時刻$t$における目的値(sin波の値)は、$(t-100)$~$(t-1)$の入力データ(sin波にノイズがのった入力)から予測されるものと考えます。
実際の事例として気温を予測するような例に当てはめてみると、過去の気温から現在の気温を予測するようなイメージを持ってもらえるといいかと思います。実際には、入力として過去の気温、気圧、湿度、…というように複数の特徴を使うことも考えられます。その時には、ある時刻に入力するデータの特徴数が増えることになります。今回は、シンプルにするために入力の特徴は1つだけとして考えます。
実装例
以下に、TensorFlow/Kerasを用いたSimpleRNNの実装例を示します。
import matplotlib.pyplot as plt
import numpy as np
from tensorflow import keras
from tensorflow.keras import layers
def main():
"""メイン関数"""
np.random.seed(1)
# ===== データ準備
data_len = 1000
t = np.arange(data_len)
y = np.sin(20 * np.pi * t / data_len)
noise = 0.1 * np.random.randn(data_len)
input_data = y + noise
# データを訓練用、評価用、テスト用に分割する
num_train_samples = int(0.5 * input_data.shape[0])
num_val_samples = int(0.25 * input_data.shape[0])
num_test_samples = int(0.25 * input_data.shape[0])
print(num_train_samples, num_val_samples, num_test_samples)
# データを描画する
plt.plot(t, input_data, "b", label="data")
plt.plot(t, y, "r", label="true")
plt.legend()
plt.show()
# ===== データセットを作成する
# データのサンプリング、シーケンス、バッチサイズの設定
sampling_rate = 1
sequence_length = 100
sequence_stride = 1
batch_size = 32
# 訓練用データセット
x_train = input_data[0:num_train_samples]
y_train = y[sampling_rate * sequence_length :]
train_dataset = keras.utils.timeseries_dataset_from_array(
x_train,
targets=y_train,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=True,
batch_size=batch_size,
)
# 評価用データセット
x_val = input_data[num_train_samples : num_train_samples + num_test_samples]
y_val = y[num_train_samples + sampling_rate * sequence_length :]
val_dataset = keras.utils.timeseries_dataset_from_array(
x_val,
targets=y_val,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=True,
batch_size=batch_size,
)
# テスト用データセット
x_test = input_data[num_train_samples + num_val_samples :]
y_test = y[num_train_samples + num_val_samples + sampling_rate * sequence_length :]
test_dataset = keras.utils.timeseries_dataset_from_array(
x_test,
targets=y_test,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=False,
batch_size=batch_size,
)
# ===== SimpleRNNのモデルを構築する
inputs = keras.Input(shape=(sequence_length, 1))
x = layers.SimpleRNN(16, return_sequences=False)(inputs)
outputs = layers.Dense(1)(x)
# ===== モデルを構築する
model = keras.Model(inputs, outputs)
# ===== オプティマイザ、損失関数、指標を設定してコンパイル
model.compile(optimizer="adam", loss="mse", metrics=["mae"])
print(model.summary())
# ===== モデルの訓練
epochs = 50
callbacks = [
keras.callbacks.ModelCheckpoint("simple_rnn.keras", save_best_only=True)
]
# 訓練の実行
history = model.fit(
train_dataset, epochs=epochs, validation_data=val_dataset, callbacks=callbacks
)
# ===== history情報の可視化
# 誤差(Mean Absolute Error)の履歴
mae = history.history["mae"]
val_mae = history.history["val_mae"]
# 誤差履歴描画
x_epoch = range(1, epochs + 1)
plt.plot(x_epoch, mae, "r", label="training mae")
plt.plot(x_epoch, val_mae, "b", label="validation mae")
plt.xlabel("Epochs")
plt.ylabel("Mean Absolute Error")
plt.legend()
# ===== evaluateを使ったテストデータでの評価
model = keras.models.load_model("simple_rnn.keras")
result = model.evaluate(test_dataset)
print(result)
# ===== predictを使って予測
preds = model.predict(test_dataset)
plt.figure()
test_start_idx = num_train_samples + num_val_samples
plt.plot(t[test_start_idx:], input_data[test_start_idx:], "b", label="data")
plt.plot(t[test_start_idx:], y[test_start_idx:], "r", label="true")
plt.plot(
t[test_start_idx + sampling_rate * sequence_length :],
preds,
"g",
label="prediction",
)
plt.legend()
plt.show()
if __name__ == "__main__":
main()
【データ】sin波にノイズを加えたデータ
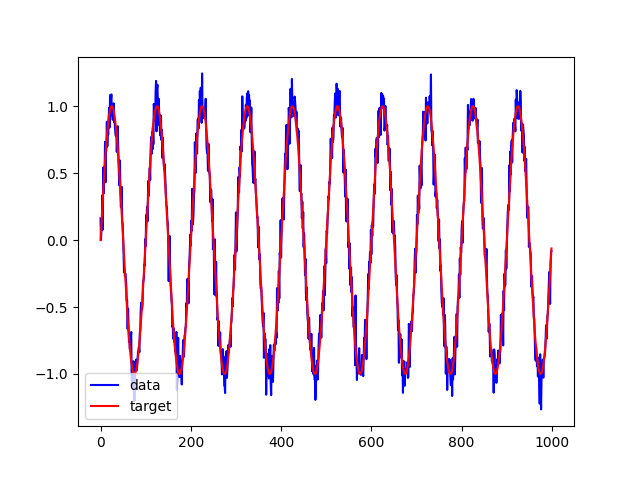
【50エポック学習した場合】
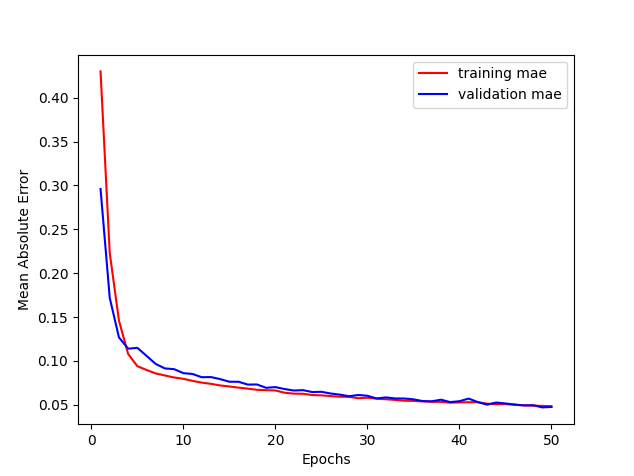
【1,000エポック実行した場合】
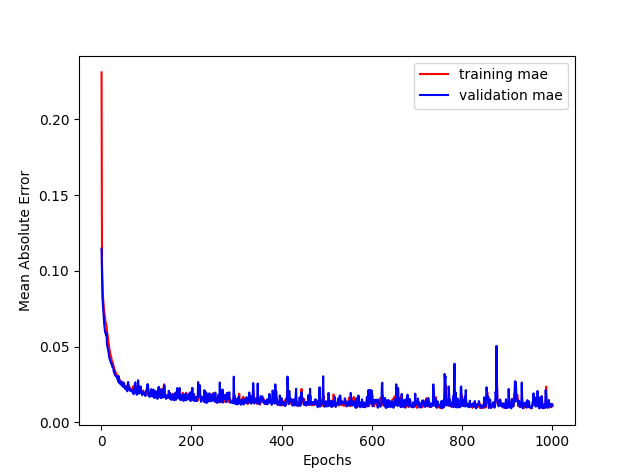
エポック数50程度だと予測線の緑線は少しギザギザしているのですが、1,000エポック実行すると、真のsin波に近い直線が予測できていることが分かります。なお、予測線の緑線が850~になっていますが、これは850の点の予測は、750~849の入力データ(青線)をもとに予測をしているためです。
実装内容の解説
上記で紹介した実装例の各部分ごとの内容を説明していきます。
必要モジュールのインポート
import matplotlib.pyplot as plt import numpy as np from tensorflow import keras from tensorflow.keras import layers
まずは、必要なモジュール類のインポートをします。今回使用するSimpleRNNは、tensorflow.keras.layersにあるためインポートしておきます。
データの用意
np.random.seed(1)
# ===== データ準備
data_len = 1000
t = np.arange(data_len)
y = np.sin(20 * np.pi * t / data_len)
noise = 0.1 * np.random.randn(data_len)
input_data = y + noise
# データを訓練用、評価用、テスト用に分割する
num_train_samples = int(0.5 * input_data.shape[0])
num_val_samples = int(0.25 * input_data.shape[0])
num_test_samples = int(0.25 * input_data.shape[0])
print(num_train_samples, num_val_samples, num_test_samples)
# データを描画する
plt.plot(t, input_data, "b", label="data")
plt.plot(t, y, "r", label="true")
plt.legend()
plt.show()
ここの部分では、使用するデータを用意しています。50%を訓練用、25%を検証用、25%をテスト用として使うことにします。RNNで訓練・検証した後、テスト用部分の入力データ（青線）を入力して、目的値（赤線）が予測できるかを確認します。
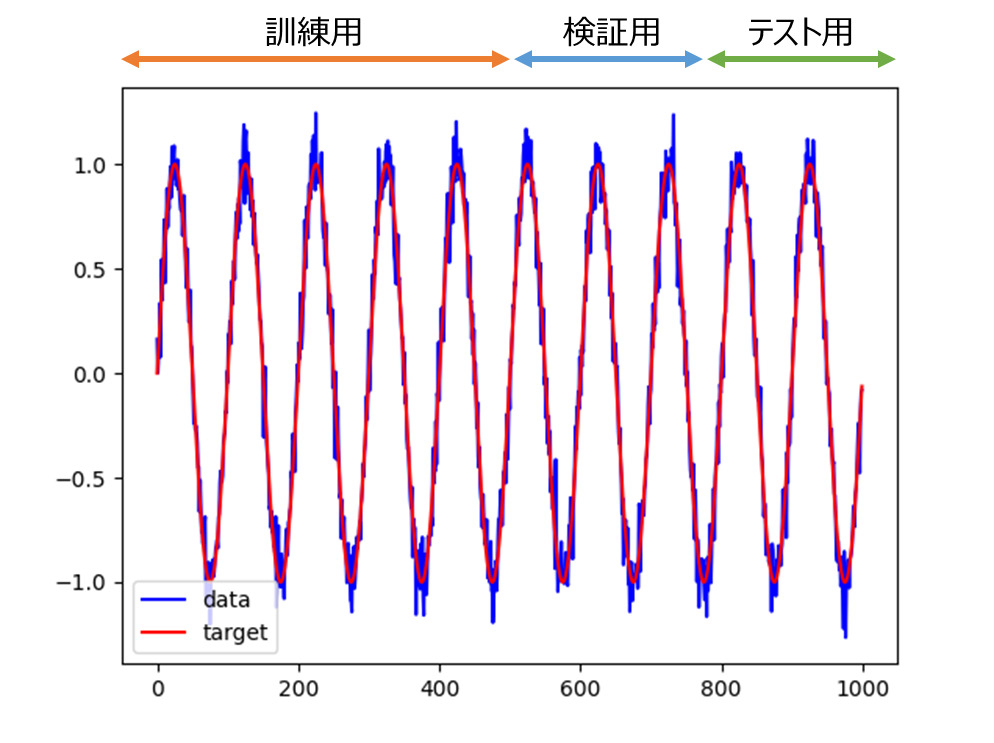
keras.utils.timeseries_dataset_from_arrayによるデータセットの構築
# ===== データセットを作成する
# データのサンプリング、シーケンス、バッチサイズの設定
sampling_rate = 1
sequence_length = 100
sequence_stride = 1
batch_size = 32
# 訓練用データセット
x_train = input_data[0:num_train_samples]
y_train = y[sampling_rate * sequence_length :]
train_dataset = keras.utils.timeseries_dataset_from_array(
x_train,
targets=y_train,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=True,
batch_size=batch_size,
)
# 評価用データセット
x_val = input_data[num_train_samples : num_train_samples + num_test_samples]
y_val = y[num_train_samples + sampling_rate * sequence_length :]
val_dataset = keras.utils.timeseries_dataset_from_array(
x_val,
targets=y_val,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=True,
batch_size=batch_size,
)
# テスト用データセット
x_test = input_data[num_train_samples + num_val_samples :]
y_test = y[num_train_samples + num_val_samples + sampling_rate * sequence_length :]
test_dataset = keras.utils.timeseries_dataset_from_array(
x_test,
targets=y_test,
sampling_rate=sampling_rate,
sequence_length=sequence_length,
sequence_stride=sequence_stride,
shuffle=False,
batch_size=batch_size,
)
時系列データを使う場合には、データシーケンスを作る必要があります。少しずつ時間をずらしたデータセットを作成するのは面倒ですが、時系列のデータセットを作る場合には、keras.utils.timeseries_dataset_from_arrayが使用できます。引数としては以下のようなものがあります。
- sampling_rate：サンプリングする間隔を指定する
- sequence_length：シーケンス長を指定する
- sequence_stride：シーケンスをスライドする間隔を指定する
- shuffle：Trueにするとバッチのシーケンスはシャッフルされる（i番目のシーケンスとi+1番目のシーケンスが時間的に並んでいるとは限らなくなる）
- batch_size：バッチサイズを指定する
例えば、設備から取得したデータなどはミリ秒や秒単位等の短い間隔のデータだったりしますが、周期性を考えた場合、1時間単位のデータを使って予測モデルを作りたいというようなこともあると思います。このような時には、sampling_rateをうまく使うと必要なデータ点をサンプリングできて便利です。テストデータは最後に評価するときに順番に並んでいてくれた方が分かりやすいかなと思うのでshuffle=Falseにしています。
今回の例では、sequence_length=100として現在時点の予測に直前の100点のデータを使用しています。シンプルにするためにsampling_rateとsequence_strideは共に1にしています。また、各データセットの最初100点は使えないため、目的値のyは最初の100点を除いて渡しています。
keras.utils.timeseries_dataset_from_arrayの公式ドキュメントはこちらを参照してください。
SimpleRNNモデルの構築
# ===== SimpleRNNのモデルを構築する
inputs = keras.Input(shape=(sequence_length, 1))
x = layers.SimpleRNN(16, return_sequences=False)(inputs)
outputs = layers.Dense(1)(x)
# ===== モデルを構築する
model = keras.Model(inputs, outputs)
今回の入力は、sequence_lengthなので、shapeは(sequence_length, 1)にしています。特徴がもし複数ある場合（例えば気温、気圧、湿度、…）のようなときは、1の部分が特徴数になります。
RNN層は、SimpleRNNで簡単に追加することができます。RNNには、各入力に対する出力を出す場合と、各入力シーケンスの最後の出力だけ返す場合がある事を前半で記載しましたが、return_sequence=Trueの場合は、各時刻における出力を含むシーケンスが返されます。一方で、return_sequenc=Falseとすると最後の出力だけを返します。
今回は過去データから現在時刻のデータを予測することを考えるのでreturn_sequence=Falseとしています。
モデルの訓練～評価
# ===== オプティマイザ、損失関数、指標を設定してコンパイル
model.compile(optimizer="adam", loss="mse", metrics=["mae"])
print(model.summary())
# ===== モデルの訓練
epochs = 50
callbacks = [
keras.callbacks.ModelCheckpoint("simple_rnn.keras", save_best_only=True)
]
# 訓練の実行
history = model.fit(
train_dataset, epochs=epochs, validation_data=val_dataset, callbacks=callbacks
)
# ===== history情報の可視化
# 誤差(Mean Absolute Error)の履歴
mae = history.history["mae"]
val_mae = history.history["val_mae"]
# 誤差履歴描画
x_epoch = range(1, epochs + 1)
plt.plot(x_epoch, mae, "r", label="training mae")
plt.plot(x_epoch, val_mae, "b", label="validation mae")
plt.xlabel("Epochs")
plt.ylabel("Mean Absolute Error")
plt.legend()
# ===== evaluateを使ったテストデータでの評価
model = keras.models.load_model("simple_rnn.keras")
result = model.evaluate(test_dataset)
print(result)
compile, fit, evaluateを用いたコンパイル、訓練、評価の流れについては、TensorFlow/Kerasの一般的なワークフローです。指標としては、MAE(Mean Absolute Error）を使用します。
# ===== predictを使って予測
preds = model.predict(test_dataset)
plt.figure()
test_start_idx = num_train_samples + num_val_samples
plt.plot(t[test_start_idx:], input_data[test_start_idx:], "b", label="data")
plt.plot(t[test_start_idx:], y[test_start_idx:], "r", label="true")
plt.plot(
t[test_start_idx + sampling_rate * sequence_length :],
preds,
"g",
label="prediction",
)
plt.legend()
plt.show()
最後に上記の部分ではpredictを使って予測波形を計算して表示しています。上記でも見たように、1,000エポック訓練すると、テストデータに対してもかなり目的値のSin波に近い予測ができていることが分かります。
以上が、TensorFlow/Kerasを用いてRNNを実行するための実装例です。より高度なLSTMやGRUについてもSimpleRNNと同じように使用でき、実際のところはLSTM等の方が一般的に使用されます。また別記事で整理しようかと思います。
まとめ
時系列データに対するディープラーニングモデルとしてRNN（Recurrent Neural Network：リカレントニューラルネットワーク）の概要とTensorFlow/KerasのSimpleRNNを用いた実装例について紹介してきました。
簡単なSin波を使った例で紹介してきましたが、例えば気圧や湿度などの情報から気温を予測するような例でも同じように適用を検討できます。RNNは時系列データに対する有効なモデルであるため、是非色々と試してもらえたらと思います。
上記で紹介しているソースコードについてはgithubにて公開しています。参考にしていただければと思います。
「Pythonによるディープラーニング」はTensorFlow/Kerasの中～上級者向けの本ですが非常におすすめです。CNN, RNN, Transformer, GAN等高度なモデルも扱っており面白い＆TensorFlow/Kerasの実装力をつけることができます。
