TensorFlow/Kerasを用いて変分自己符号化器(VAE:VariationalAutoEncoder)を構築し、MNISTの手書き文字データに適用する実装例について解説します。
Contents
変分自己符号化器(VAE:VariationalAutoEncoder)
変分自己符号化器(VAE:VariationalAutoEncoder)は、生成モデルの一種でベースとして、自己符号化器(AutoEncoder)の考え方がもとになっています。TensorFlow/Kerasでの自己符号化器の実装については、「自己符号化器(AutoEncoder)の実装」でまとめていますので参考にしてください。
本記事では、生成モデルである変分自己符号化器(VAE)の概要を説明した上で、TensorFlow/Kerasを用いてMNIST手書き画像に適用する実装例について紹介していきます。
変分自己符号化器(VAE)では、自己符号化器と同様に入力データを復元するように学習をするのですが、異なる点として、Encoderは入力$x$から正規分布(ガウス分布)$\mathcal{N}$の平均$\mu$と標準偏差$\sigma$を求め、その正規分布から隠れ変数の$z$をサンプリングします。
図にしてみると以下のような形になります。
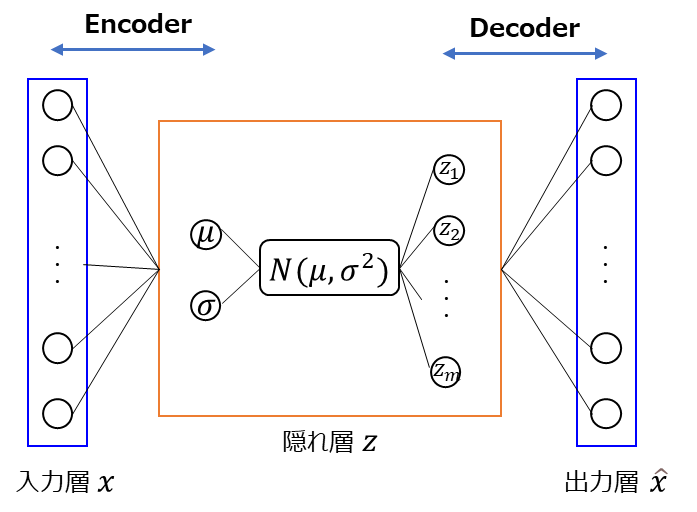
$\boldsymbol{z}$に関するサンプリングは、以下の式のように表現されます。
\[
\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})
\]
ここでいう$\boldsymbol{\mu}$は平均ベクトル、$\boldsymbol{\sigma}^{2}$は分散ベクトルです。例えば、隠れ変数$z$の次元を2次元とした場合には、平均ベクトルや分散ベクトルもそれぞれ2次元になります。
考え方としては上記なのですが、ニューラルネットワークの実装を考えたときにサンプリングが含まれると計算グラフが途切れてしまい誤差逆伝播ができないという問題があります。それに対応するために変分自己符号化器(VAE)では、後述するReparameterization Trickという手法を用います。
Reparameterization Trick
変分自己符号化器(VAE)は、自己符号化器(AutoEncoder)とは異なり$z$を正規分布(ガウス分布)からサンプリングするため、計算グラフが途切れてしまい誤差逆伝播ができないという問題があります。
これに対応するために、変分自己符号化器(VAE)では、Reparameterization Trickという手法を用います。Reparameterization Trickでは、$z$をサンプリングする代わりに、ランダムノイズ$\epsilon$をサンプリングし、$\boldsymbol{z} = \boldsymbol{\mu} + \epsilon\boldsymbol{\sigma}$という計算にします。
図にしてみると以下のようになります。
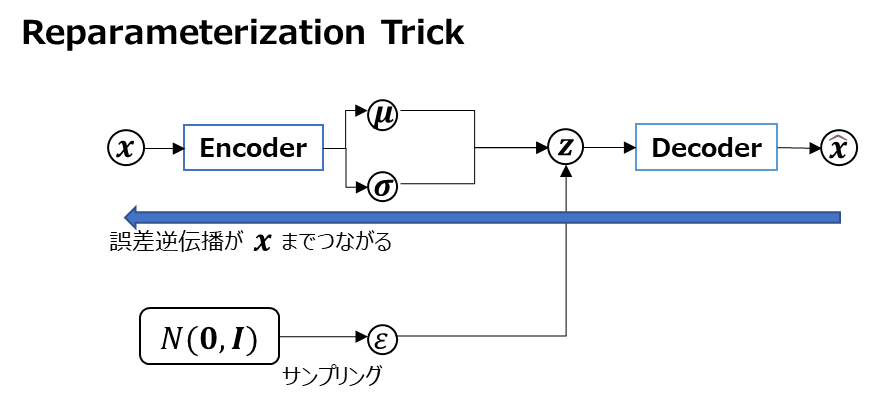
このようにReparameterization Trickを使うことで、計算グラフがつながり誤差逆伝播が可能になります。
損失関数にKLダイバージェンスを使用
変分自己符号化器(VAE)では、自己符号化器(AutoEncoder)と損失関数にも違いがあります。自己符号化器では、単純に入力画像と出力画像の誤差を’binary_crossentropy’で計算していましたが、変分自己符号化器(VAE)では、以下のKLダイバージェンスの正則化項を加えます。
\[
D_{KL}[\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})][\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})]
\]
正規分布間におけるKLダイバージェンスについては、「正規分布間のKLダイバージェンス(Kullback-Leibler divergence)の導出」で式変形を整理してみていますので、詳細が確認したい方は参考にしてください。
KLダイバージェンスは二つの分布の近さを表すようなものとなっており、0になるときに分布は完全に一致します。つまり、上記項を最小化していくことはは、隠れ変数$\boldsymbol{z}$の分布を平均$\boldsymbol{0}$、分散$\boldsymbol{I}$の標準正規分布に近づけるような働きをします。
$p(x) = \mathcal{N}(x|\mu_{1}, \sigma^{2}_{1})$、$q(x) = \mathcal{N}(x|\mu_{2}, \sigma^{2}_{2})$とするときの正規分布間のKLダイバージェンスの式は以下のようになります。
\[
\begin{eqnarray}
D_{KL}[p(x)][q(x)] &=&
\int_{-\infty}^{\infty}p(x) \log \frac{p(x)}{q(x)}dx \\
&=&
\frac{1}{2}\left( \log\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} + \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} + \frac{(\mu_{1} – \mu_{2})^{2}}{\sigma_{2}^{2}} – 1 \right)
\end{eqnarray}
\]
この式を使うと変分自己符号化器(VAE)の正規化項$D_{KL}[\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})][\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})]$は以下のようになります。
\[
\begin{eqnarray}
D_{KL}[\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})][\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})]
&=&
\frac{1}{2}\left( -\log\boldsymbol{\sigma}^{2} + \boldsymbol{\sigma}^{2} + \boldsymbol{\mu}^{2} -1 \right)
\end{eqnarray}
\]
以降の実装の中にも上記式が出てきますので理解しておいてもらえるとよいかと思います。
TensorFlow/Kerasでの変分自己符号化器(VAE:VariationalAutoEncoder)の実装
変分自己符号化器(VAE)を使用したTensorFlow/Kerasでの実装例を紹介します。今回は、MNISTの手書き文字データに対して適用する例を考えてみたいと思います。
隠れ変数$\boldsymbol{z}$の次元数は2次元で実装し、後で2次元の$\boldsymbol{z}$の各点に対してデコーダで画像を生成して表示します。プログラム中のlatent_dimを変えれば3次元以上にすることももちろん可能です。
実装例
変分自己符号化器(VAE)のTensoflow/Kerasを用いた実装例を以下に紹介します。
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.datasets import mnist
class VAE(keras.Model):
"""VAE (Variational Auto Encoder)モデル"""
def __init__(self, encoder, decoder, **kwargs):
"""コンストラクタ
Args:
encoder: エンコーダー
decoder: デコーダー
"""
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.sampler = Sampler()
# 損失関数トレース用
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.kl_loss_tracker,
]
def train_step(self, data):
"""訓練ステップ
Args:
data: 入力データ
Returns:
損失値 (total_loss, reconstruction_loss, kl_loss)
"""
with tf.GradientTape() as tape:
z_mean, z_log_var = self.encoder(data)
z = self.sampler(z_mean, z_log_var)
reconstructed_data = self.decoder(z)
# 誤差の計算
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstructed_data),
axis=(1, 2),
)
)
# KLダイバージェンス
kl_loss = 0.5 * (-z_log_var + tf.exp(z_log_var) + tf.square(z_mean) - 1)
# 総誤差
total_loss = reconstruction_loss + kl_loss
# 勾配計算
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
# 誤差の設定
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
ret = {
"total_loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
return ret
class Sampler(layers.Layer):
"""潜在変数zのサンプル実行クラス"""
def call(self, z_mean, z_log_var):
"""実行関数
Args:
z_mean: 平均
z_log_var: 分散(対数)
Returns:
サンプリング値
"""
batch_size = tf.shape(z_mean)[0]
z_size = tf.shape(z_mean)[1]
# 正規ガウス分布からランダムな値(epsilon)を抽出
epsilon = tf.random.normal(shape=(batch_size, z_size))
# サンプリング値を使用してzを計算して返却
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
def main():
"""メイン関数"""
# ===== MNIST(エムニスト)データの読込
(train_imgs, _), (test_imgs, _) = mnist.load_data()
# 全ての画像を使って生成モデルを訓練するため訓練データとテストデータを結合
train_imgs = np.concatenate([train_imgs, test_imgs], axis=0)
# reshapeと正規化(0~1)
train_imgs = train_imgs.reshape((70000, 28, 28, 1)).astype("float32") / 255
# ===== Encoder(エンコーダ)ネットワークの構築
# 2次元の潜在空間
latent_dim = 2
# ネットワークの構築
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(
encoder_inputs
)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
# 平均と分散
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var")(x)
# Encoderモデルの構築
encoder = keras.Model(
inputs=encoder_inputs, outputs=[z_mean, z_log_var], name="encoder"
)
print(encoder.summary())
keras.utils.plot_model(encoder, "encoder.png", show_shapes=True)
# ===== Decoder(デコーダ)ネットワークの構築
latent_inputs = keras.Input(shape=(latent_dim,))
# ネットワークの構築
# Encoderと逆の手順で画像に戻していく
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
# 最終的には元画像と同じ(28, 28, 1)の形状にする
decoder_outputs = layers.Conv2D(1, 3, activation="sigmoid", padding="same")(x)
# Decoderモデルの構築
decoder = keras.Model(inputs=latent_inputs, outputs=decoder_outputs, name="decoder")
print(decoder.summary())
keras.utils.plot_model(decoder, "decoder.png", show_shapes=True)
# ===== VAEモデルの生成
vae = VAE(encoder, decoder)
# ===== モデルのコンパイル
vae.compile(optimizer="adam", run_eagerly=True)
# ===== モデルの学習
n_epochs = 30
history = vae.fit(train_imgs, epochs=n_epochs, batch_size=128)
# ===== 潜在空間のサンプルから画像を生成する
n_imgs = 30
img_size = 28
figure_data = np.zeros((img_size * n_imgs, img_size * n_imgs))
# 潜在変数zのグリッド
z_grid_1 = np.linspace(-1, 1, n_imgs)
z_grid_2 = np.linspace(-1, 1, n_imgs)
# 各z点における画像を生成モデルから作成
for i, z_1 in enumerate(z_grid_1):
for j, z_2 in enumerate(z_grid_2):
z = np.array([[z_1, z_2]])
decoded_img = vae.decoder.predict(z)
img = decoded_img[0].reshape(img_size, img_size)
# figure_dataの該当位置に埋め込み
figure_data[
i * img_size : (i + 1) * img_size, j * img_size : (j + 1) * img_size
] = img
# 軸の値を生成
start_range = img_size // 2
end_range = n_imgs * img_size + start_range
pixel_range = np.arange(start_range, end_range, img_size)
sample_range_x = np.round(z_grid_1, 1)
sample_range_y = np.round(z_grid_2, 1)
# 生成画像の表示
plt.figure(figsize=(10, 10))
plt.imshow(figure_data)
plt.xticks(pixel_range, sample_range_x)
plt.yticks(pixel_range, sample_range_y)
plt.xlabel("z[0]")
plt.ylabel("z[1]")
plt.gray()
plt.savefig("result.png")
plt.show()
if __name__ == "__main__":
main()【実行結果例】

実装内容の解説
上記で紹介した実装例の各部分ごとに内容を紹介していきます。少し長くなりますが順を追って確認してもらえれば理解が深まるかと思います。
Encoder(エンコーダ)の定義
# ===== Encoder(エンコーダ)ネットワークの構築
# 2次元の潜在空間
latent_dim = 2
# ネットワークの構築
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(
encoder_inputs
)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
# 平均と分散
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var")(x)
# Encoderモデルの構築
encoder = keras.Model(
inputs=encoder_inputs, outputs=[z_mean, z_log_var], name="encoder"
)
print(encoder.summary())
keras.utils.plot_model(encoder, "encoder.png", show_shapes=True)変分自己符号化器(VAE)におけるEncoder(エンコーダ)のネットワークを定義している部分です。
潜在変数の次元は「latent_dim」=2ということにしているため、$\boldsymbol{z}$の次元は2次元になります。今回はMNIST画像(28×28)でグレースケールなのでチャンネルは1です。ニューラルネットワークの層は、Conv2Dの単純なCNNによる層になっています。
通常のCNNだと、畳み込み層とプーリング層を繰り返していきますが、今回はストライドが2の畳み込み層のみで構成されているのがポイントです。畳み込み層は局所的な情報を抽出するもので、プーリング層は情報の損失を抑えつつデータを圧縮しているものでした。この特徴からプーリング層を使うと局所的な情報が消えてしまいます。今回は画像を復元することが目的であるため局所的な情報が消えていってしまうことは望ましくありません。このような時には、ストライドを使ってダウンサンプリングしていくテクニックを使用します。
畳み込み層をかけた後に、Flatten()で平坦化した後に全結合層を通じてz_meanとz_log_varに接続します。ここでは$\boldsymbol{\mu}$と$\log\boldsymbol{\sigma}^{2}$に変換するように作っています。
summary()とplot_modelでEncoder(エンコーダ)モデルの構成を見てみると以下のようになっています。
Model: "encoder"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, 28, 28, 1)] 0 []
conv2d (Conv2D) (None, 14, 14, 32) 320 ['input_1[0][0]']
conv2d_1 (Conv2D) (None, 7, 7, 64) 18496 ['conv2d[0][0]']
flatten (Flatten) (None, 3136) 0 ['conv2d_1[0][0]']
dense (Dense) (None, 16) 50192 ['flatten[0][0]']
z_mean (Dense) (None, 2) 34 ['dense[0][0]']
z_log_var (Dense) (None, 2) 34 ['dense[0][0]']
==================================================================================================
Total params: 69,076
Trainable params: 69,076
Non-trainable params: 0
__________________________________________________________________________________________________
None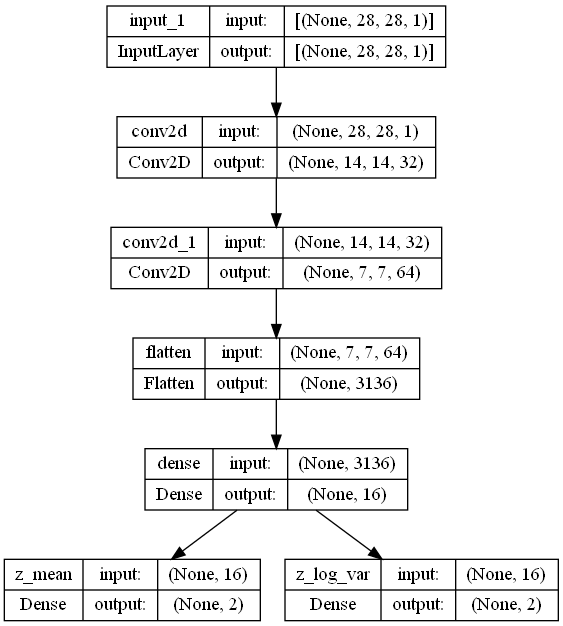
plot_modelで図示してみると、入力から順次畳み込みが行われて最後に2つに分岐しているのがよく分かるかと思います。これで、Encoder(エンコーダ)部の定義が完了です。
padding=’same’というのは元の画像とサイズが一致するようにパディングする設定なので、ダウンサンプリングされていることが気になる方もいるかもしれません。(私は最初そうでした)
CNNの画像サイズに関する有名な式として以下のような式があります。画像の幅・高さを$W$、フィルタサイズ$F$、ストライド$S$、パディング$P$としたときのCNNをかけた後の出力画像サイズです。
\[
\left(\frac{W+2P-F}{S} + 1\right) \times \left(\frac{W+2P-F}{S} + 1\right)
\]
padding=’same’の設定は、ストライド$S=1$の時に画像サイズが入力と同じになるように調整されます。つまりは、分子が入力と同じになるように$P$が設定されます。今回の場合は、ストライド$S=2$のため画像が半分ずつになっているわけです。
Decoder(デコーダ)の定義
# ===== Decoder(デコーダ)ネットワークの構築
latent_inputs = keras.Input(shape=(latent_dim,))
# ネットワークの構築
# Encoderと逆の手順で画像に戻していく
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
# 最終的には元画像と同じ(28, 28, 1)の形状にする
decoder_outputs = layers.Conv2D(1, 3, activation="sigmoid", padding="same")(x)
# Decoderモデルの構築
decoder = keras.Model(inputs=latent_inputs, outputs=decoder_outputs, name="decoder")
print(decoder.summary())
keras.utils.plot_model(decoder, "decoder.png", show_shapes=True)変分自己符号化器(VAE)におけるDecoder(デコーダ)のネットワークを定義している部分です。
Decoder(デコーダ)の入力は、潜在変数のため入力の次元はlatent_dimになります。デコーダでは潜在変数から元画像を復元することが目的であるため、Encoder(エンコーダ)とは逆の処理を行っていきます。
Conv2DTransposeを使用し、最終的には元画像と同じ(28, 28, 1)の形状にしていきます。
summary()とplot_modelでDecoder(デコーダ)モデルの構成を見てみると以下のようになっています。
Model: "decoder"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 2)] 0
dense_1 (Dense) (None, 3136) 9408
reshape (Reshape) (None, 7, 7, 64) 0
conv2d_transpose (Conv2DTra (None, 14, 14, 64) 36928
nspose)
conv2d_transpose_1 (Conv2DT (None, 28, 28, 32) 18464
ranspose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 289
=================================================================
Total params: 65,089
Trainable params: 65,089
Non-trainable params: 0
_________________________________________________________________
None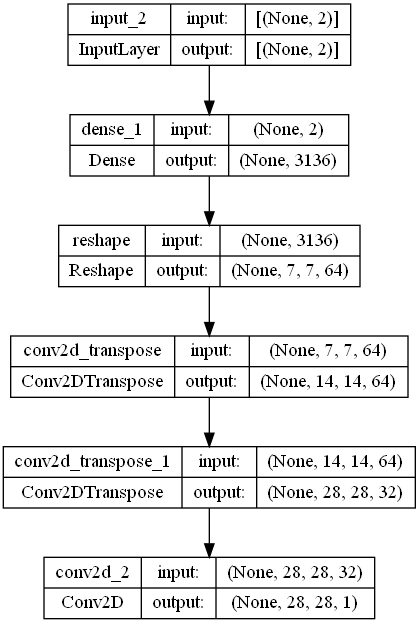
plot_modelで図示してみると、最終的に(28, 28, 1)の元画像と同じサイズの画像に変換されて行っていることがよく分かるかと思います。これで、Decoder(デコーダ)部の定義が完了です。
サンプリング用のレイヤークラスの定義
class Sampler(layers.Layer):
"""潜在変数zのサンプル実行クラス"""
def call(self, z_mean, z_log_var):
"""実行関数
Args:
z_mean: 平均
z_log_var: 分散(対数)
Returns:
サンプリング値
"""
batch_size = tf.shape(z_mean)[0]
z_size = tf.shape(z_mean)[1]
# 正規ガウス分布からランダムな値(epsilon)を抽出
epsilon = tf.random.normal(shape=(batch_size, z_size))
# サンプリング値を使用してzを計算して返却
return z_mean + tf.exp(0.5 * z_log_var) * epsilonEncoder(エンコーダ)とDecoder(デコーダ)が定義できたので、$\boldsymbol{z}$のサンプリングに関するレイヤークラスを定義します。
クラスはtensorflow.keras.layers.Layerクラスを継承して作成します。batch_sizeは、入力された画像数で、z_sizeは$\boldsymbol{z}$の次元数(今回は2)になります。
上記で説明した通り$\boldsymbol{z}$を直接サンプリングするのではなく、$\epsilon$を平均0、分散1の正規分布からサンプリングした上で、以下の式でzを計算します。
\[
\begin{eqnarray}
\boldsymbol{z} = \boldsymbol{\mu} + \epsilon\boldsymbol{\sigma}\\
\epsilon \sim \mathcal{N}(0, 1)
\end{eqnarray}
\]
エンコーダでは、$\log\boldsymbol{\sigma}^2$を生成しているので、tf.exp(0.5 * z_log_var)の部分は$\boldsymbol{\sigma}$ということになります。これで、$\boldsymbol{z}$に関するサンプリングが実行できます。
変分自己符号化器(VAE)クラスの定義
さて、Encoder(エンコーダ)、Decoder(デコーダ)、サンプリング層といった変分自己符号化器(VAE)の構成部品ができたので、実際のVAEクラスを定義していきます。
class VAE(keras.Model):
"""VAE (Variational Auto Encoder)モデル"""
def __init__(self, encoder, decoder, **kwargs):
"""コンストラクタ
Args:
encoder: エンコーダー
decoder: デコーダー
"""
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.sampler = Sampler()
# 損失関数トレース用
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.kl_loss_tracker,
]
def train_step(self, data):
"""訓練ステップ
Args:
data: 入力データ
Returns:
損失値 (total_loss, reconstruction_loss, kl_loss)
"""
with tf.GradientTape() as tape:
z_mean, z_log_var = self.encoder(data)
z = self.sampler(z_mean, z_log_var)
reconstructed_data = self.decoder(z)
# 誤差の計算
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstructed_data),
axis=(1, 2),
)
)
# KLダイバージェンス
kl_loss = 0.5 * (-z_log_var + tf.exp(z_log_var) + tf.square(z_mean) - 1)
# 総誤差
total_loss = reconstruction_loss + kl_loss
# 勾配計算
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
# 誤差の設定
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
ret = {
"total_loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
return retVAEクラスは、tensorflow.keras.Modelを継承して作成します。このクラスは少し長いのでさらに部分的に説明をしていきます。
コンストラクタ __init__
def __init__(self, encoder, decoder, **kwargs):
"""コンストラクタ
Args:
encoder: エンコーダー
decoder: デコーダー
"""
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.sampler = Sampler()
# 損失関数トレース用
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")VAEクラスは、Encoder(エンコーダ)とDecoder(デコーダ)を受け取って設定します。
また、損失関数のトレースのためにtensorflow.keras.metrics.Meanで損失関数の値を記録するものを総損失(total_loss)、再構成誤差(reconstruction_loss)、LKダイバージェンスの損失(kl_loss)ということで用意しています。Meanでは、後で出てきますがupdate_stateメソッドで平均値を計算することができます。
metricsメソッド
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.kl_loss_tracker,
]この@propertyデコレータがついているmetricsメソッドで指標を定義しておくことで、fit()やevaluate()を呼び出すたびにモデルが指標をリセットするように動作するようになります。
train_stepメソッド(訓練ステップ)
def train_step(self, data):
"""訓練ステップ
Args:
data: 入力データ
Returns:
損失値 (total_loss, reconstruction_loss, kl_loss)
"""
with tf.GradientTape() as tape:
z_mean, z_log_var = self.encoder(data)
z = self.sampler(z_mean, z_log_var)
reconstructed_data = self.decoder(z)
# 誤差の計算
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstructed_data),
axis=(1, 2),
)
)
# KLダイバージェンス
kl_loss = 0.5 * (-z_log_var + tf.exp(z_log_var) + tf.square(z_mean) - 1)
# 総誤差
total_loss = reconstruction_loss + kl_loss
# 勾配計算
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
# 誤差の設定
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
ret = {
"total_loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
return rettrain_stepメソッドでは、実際の訓練の動作を定義します。
with tf.GradientTape() as tape:
# ~順伝搬の計算(省略)
# 勾配計算
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))順伝播の処理を記載する部分については、誤差の勾配が計算できるように「with tf.GradientTape() as tape:」内に記載します。これによりtape.gradientで勾配を計算し、optimizer.apply_gradientsで重みに対して勾配を適用できます。この流れは、tensorflowで勾配計算して重みに反映する一般的な構成です。
z_mean, z_log_var = self.encoder(data)
z = self.sampler(z_mean, z_log_var)
reconstructed_data = self.decoder(z)では、具体的に順伝搬の中身を見てみます。まずは上記の部分で、encoder→sampler→decoderという順に入力データに対してこれまでに構成した処理を適用し、出力の再構成データ(reconstructed_data)を生成します。
# 誤差の計算
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstructed_data),
axis=(1, 2)
)
)入力との誤差を求めているのが上記の部分です。この部分では、binary_crossentropyで入力(data)と再構成データ(reconstructed_data)を計算しています。reduce_sumでaxisの(1, 2)を指定しているので画像内で平均をとっており、その後、reduce_meanをとっているのでバッチ内の画像全てで平均をとっていることになります。
# KLダイバージェンス
kl_loss = 0.5 * (-z_log_var + tf.exp(z_log_var) + tf.square(z_mean) - 1)この部分では、KLダイバージェンスで$\boldsymbol{z}$の分布が、$\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$に近づくようにするための項目です。
上記に正規分布間のKLダイバージェンスの式について紹介しましたが、その通りになっているのがよく見ていただけると分かるかと思います。
\[
\begin{eqnarray}
D_{KL}[\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})][\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})]
&=&
\frac{1}{2}\left( -\log\boldsymbol{\sigma}^{2} + \boldsymbol{\sigma}^{2} + \boldsymbol{\mu}^{2} -1 \right)
\end{eqnarray}
\]
printなどしてみてもらえれば分かりますがこの時点では、kl_lossは(batch_size, z_size)の形状をしています。Meanのupdate_stateに入る時点で全体の平均に変わります。
# 総誤差
total_loss = reconstruction_loss + kl_loss総誤差として、再構成誤差とKLダイバージェンスの値を合計して指標とします。
# 誤差の設定
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
ret = {
"total_loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
return ret最後に、指標のtrackerにそれぞれ値を設定して、最後にreturnしています。
以上が、VAEクラスの内容の概要説明になります。
実行部分(main)の内容
では、最後に全体の処理を実行しているmain部分について説明します。
MNISTデータの準備
# ===== MNIST(エムニスト)データの読込
(train_imgs, _), (test_imgs, _) = mnist.load_data()
# 全ての画像を使って生成モデルを訓練するため訓練データとテストデータを結合
train_imgs = np.concatenate([train_imgs, test_imgs], axis=0)
# reshapeと正規化(0~1)
train_imgs = train_imgs.reshape((70000, 28, 28, 1)).astype("float32") / 255今回対象とするMNISTデータを読み込んでいる部分です。今回生成モデルを訓練するために訓練データとテストデータは結合してまとめてしまっています。また、データとしてはreshapeして、0~1の間に入るように正規化しています。
Encoder(エンコーダ)とDecoder(デコーダ)の定義
Encoder(エンコーダ)とDecoder(デコーダ)のネットワーク定義は、main内で行ってVAEクラスに渡しています。今回はMNIST用のEncoder(エンコーダ)とDecoder(デコーダ)なので、VAEクラスの外で作成して渡す構成としています。Encoder(エンコーダ)とDecoder(デコーダ)の詳細は上記で説明しているのでそちらを参照してください。
VAEモデルの生成と訓練
# ===== VAEモデルの生成
vae = VAE(encoder, decoder)
# ===== モデルのコンパイル
vae.compile(optimizer="adam", run_eagerly=True)
# ===== モデルの学習
n_epochs = 30
history = vae.fit(train_imgs, epochs=n_epochs, batch_size=128)この部分でVAEモデルの生成~訓練(学習)までを実行しています。
VAEをインスタンス化する際には、encoderとdecoderを渡して構築します。compile時にはオプティマイザーを’adam’としました。一般的にはcompile時に損失関数を指定しますが、今回は個別にtrain_step()内で定義しているので引数としては指定しません。
また、run_eagerlyをTrueにしておくと、モデル内の処理でprintで値を表示したりすることができますのでデバッグで便利です。これを指定しないとtrain_step()メソッド内等でprintしてもテンソルの値を確認できません。
モデルの学習は、fit()を使用します。通常は、訓練データ、目的値(正解データ)という順で指定するのが一般的ですが、今回目的となる値は訓練データ自身になるため、目的値は指定しません。
ここまでで、変分自己符号化器(VAE)による生成モデルの訓練ができます。
# ===== 潜在空間のサンプルから画像を生成する
n_imgs = 30
img_size = 28
figure_data = np.zeros((img_size * n_imgs, img_size * n_imgs))
# 潜在変数zのグリッド
z_grid_1 = np.linspace(-1, 1, n_imgs)
z_grid_2 = np.linspace(-1, 1, n_imgs)
# 各z点における画像を生成モデルから作成
for i, z_1 in enumerate(z_grid_1):
for j, z_2 in enumerate(z_grid_2):
z = np.array([[z_1, z_2]])
decoded_img = vae.decoder.predict(z)
img = decoded_img[0].reshape(img_size, img_size)
# figure_dataの該当位置に埋め込み
figure_data[
i * img_size : (i + 1) * img_size, j * img_size : (j + 1) * img_size
] = img
# 軸の値を生成
start_range = img_size // 2
end_range = n_imgs * img_size + start_range
pixel_range = np.arange(start_range, end_range, img_size)
sample_range_x = np.round(z_grid_1, 1)
sample_range_y = np.round(z_grid_2, 1)
# 生成画像の表示
plt.figure(figsize=(10, 10))
plt.imshow(figure_data)
plt.xticks(pixel_range, sample_range_x)
plt.yticks(pixel_range, sample_range_y)
plt.xlabel("z[0]")
plt.ylabel("z[1]")
plt.gray()
plt.savefig("result.png")
plt.show()では、実際に訓練した変分自己符号化器(VAE)のモデルから画像を生成してみましょう。具体的には、潜在変数$\boldsymbol{z}$を任意で用意して、その$\boldsymbol{z}$に対する生成画像をdecoderを通して作成します。
潜在変数の次元(latent_dim)=2としているので、z[0]とz[1]ということで-1~1までの等間隔のデータをlinspaceで作成しています。その$\boldsymbol{z}$に対してfor文でdecoded_img = vae.decoder.predict(z)で生成しています。画像は大きな一枚の画像(figure_data)にまとめてmatplotlibで表示しています。

具体的に生成した結果画像例を再掲します。z[0]、z[1]の値に対してどのような手書き文字画像が生成されているかが位置で分かるようになっています。
乱数を使っているので結果は実行のたびに変わりますが、ここで重要なのは同じ数字は同じ位置にあり、連続的に形状が変わっているということです。例えば上記の結果だと右上は0が左下は7、真ん中あたりは3や8でしょうか、といった形で連続的に画像が変化しているのが分かります。つまり、この潜在空間の位置は0らしさ、8らしさ等のMNIST画像の分布を表すような生成空間になっているというわけです。
以上が、変分自己符号化器(VAE)の実装に関する説明でした。
まとめ
生成モデルである変分自己符号化器(VAE:VariationalAutoEncoder)の概要を説明した上で、TensorFlow/Kerasを用いてMNIST手書き画像に適用する実装例について紹介しました。
自己符号化器についても「自己符号化器(AutoEncoder)の実装」でまとめていますが、サンプリングやKLダイバージェンスを含む損失関数を計算する必要がある点が異なるため、自己符号化器より実装は複雑です。
そのため、ポイントごとに説明をしたことから少し長い記事にはなってしまいましたが、変分自己符号化器(VAE)の内容を理解するのに少しでも役立てばよいかなと思います。
上記で紹介しているソースコードについてはgithubにて公開しています。参考にしていただければと思います。
の実装.jpg)


による画像分類の基本-640x360.jpg)

の作成方法-640x360.jpg)



