【scikit-learn】LinearRegressionで線形回帰をする方法

Pythonの機械学習ライブラリであるscikit-learnのLinearRegressionを使って線形回帰をする方法について解説します。
目次
線形回帰
回帰分析は、予測したいデータに対して、既に与えられているデータから関係性を推定することを言います。この時に$x^{2}$, $x^{3}$等の累乗の形がない線形の式で予測する回帰の事を線形回帰と言います。
例えば、簡単な直線を推定することを考えてみましょう。ある$(x, y)$のデータ群が与えられていたとします。この時、線形回帰モデルとして$y=ax + b$という数式を決めて当てはめることを考えます。線形回帰では、与えられたデータ$(x, y)$から$a$と$b$は何になるかということを推定します。
$a$と$b$が分かると、与えられていない未知の$x$に対して$y$の値がどのようになるかを予測することができるようになります。
Pythonではscikit-learnという機械学習ライブラリのLinearRegressionを使用することで線形回帰ができます。以降ではLinearRegressionの使用方法について紹介します。
scikit-learnのLinearRegressionで線形回帰を実装する方法
以降では、scikit-learnを使用します。インストールがされていない場合はpipでインストールをしておいてください。
pip install scikit-learn
線形単回帰
線形単回帰とは、1つの予測したいデータ$y$を1つのデータ$x$から求める回帰分析方法です。式で表すと以下になります。
\[
y = ax + b
\]
この時、$(x, y)$の学習データがあった時に$a$や$b$を推定します。$a$は係数、$b$はバイアスとも言われます。
実装例
線形単回帰は、scikit-learnのLinearRegressionを使用して以下のようなプログラムで実行できます。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
def main():
rs = np.random.RandomState(123)
# ===== 線形回帰を行うためのデータを生成する
bias = 5.0
x, y, coef = make_regression(
n_samples=100,
n_features=1,
n_targets=1,
coef=True,
bias=bias,
noise=5.0,
random_state=rs,
)
np.set_printoptions(precision=3, suppress=True)
print(f"true coef: {coef:.3f}")
print(f"true bias: {bias:.3f}")
plt.plot(x, y, ".")
# 訓練用データとテスト用データを分割する
train_x, test_x, train_y, test_y = train_test_split(x, y, random_state=rs)
# ===== 線形単回帰モデルを生成する
model = LinearRegression(fit_intercept=True)
# ===== モデルを学習する
model.fit(train_x, train_y)
# 推定結果の表示
print(f"coef: {model.coef_}")
print(f"bias: {model.intercept_:.3f}")
print(f"R2: {model.score(test_x, test_y):.3f}")
# ===== 線形回帰結果の線を引く
xfit = np.linspace(np.min(x), np.max(x), 1000)
# Y軸はpredictを実行して計算
yfit = model.predict(xfit[:, np.newaxis])
plt.plot(xfit, yfit)
plt.show()
if __name__ == "__main__":
main()【実行結果】 true coef: 33.867 true bias: 5.000 coef: [34.185] bias: 4.611 R2: 0.982
【表示結果】
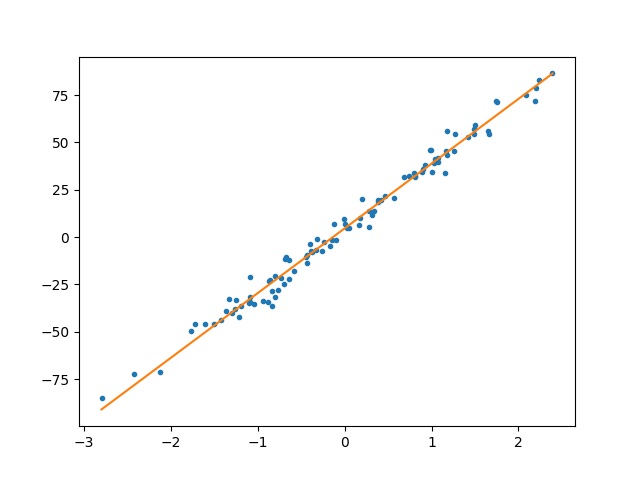
青色のプロット点が与えられたデータです。それに対して、オレンジの線がモデルに当てはめて予測した直線になります。ぱっと見でデータの特徴を捉えられた直線になっていそうだないうことは分かるのではないかなと思います。
実装内容の解説
上記で紹介した実装例の各部分ごとの内容を説明していきます。
必要モジュールのインポート
import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import make_regression from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split
まずは、各種必要なライブラリをインポートします。線形回帰については、sklearn.linear_modelからLinearRegressionをインポートします。
また、データ生成用のlinear_model.make_regression、テストデータ分割用のmodel_selection.train_test_splitもsklearnからインポートします。
numpyやmatplotlibは分析に使うデータの処理や可視化のために使用します。
データセットの用意
# ===== 線形回帰を行うためのデータを生成する
bias = 5.0
x, y, coef = make_regression(
n_samples=100,
n_features=1,
n_targets=1,
coef=True,
bias=bias,
noise=5.0,
random_state=rs,
)
np.set_printoptions(precision=3, suppress=True)
print(f"true coef: {coef:.3f}")
print(f"true bias: {bias:.3f}")
plt.plot(x, y, ".")
# 訓練用データとテスト用データを分割する
train_x, test_x, train_y, test_y = train_test_split(x, y, random_state=rs)今回は、sklearn.datasets.make_regressionを使ってデータを用意しています。各引数の意味は以下の通りです。単回帰用のデータは$x$、$y$でそれぞれ一次元なので、n_features=1, n_targets=1としています。返却されたcoefとbiasが(x, y)から予測するべき真の係数ということになります。
- n_samples: データ数
- n_features: 特徴数($x$)
- n_targets: 目標値($y$)
- coef: データを生成した線形モデルの係数を返却するか否か(True: 返却)
- bias: バイアス
- noise: データに加えるガウスノイズの標準偏差
- random_state: 乱数のシード
また、学習用データとテスト用データを分割するためにtrain_test_splitで生成したデータを分割しています。
線形回帰モデルの生成と学習
# ===== 線形単回帰モデルを生成する
model = LinearRegression(fit_intercept=True)
# ===== モデルを学習する
model.fit(train_x, train_y)
# 推定結果の表示
print(f"coef: {model.coef_}")
print(f"bias: {model.intercept_:.3f}")
print(f"R2: {model.score(test_x, test_y):.3f}")上記の部分で線形回帰モデルを生成して学習しています。fit_interceptは、Trueにすることでバイアスの予測も行います。
線形回帰を実行しているのは、fitメソッドです。学習用データのtrain_xとtrain_yを引数に渡します。線形回帰結果は、modelのcoef_とintercept_から取得することができます。結果としてはデータ生成時の真値に近い値が得られていることが分かるかと思います。
ただ、係数の単純に値が近いというだけだとどれだけの精度があるのかが評価できません。線形回帰では、予測データと実際の正解データがどれぐらい一致しているのかを示す指標として決定係数$R^{2}$というものがよく使用されます。決定係数の定義は複数ありますが、scikit-learnで計算される$R^{2}$の定義は以下の通りです。
\[
R^{2} = 1 – \frac{\sum_{i}(y_{i}-\hat{y}_{i})^{2}}{\sum_{i}(y_{i}-\bar{y})^{2}}
\]
$\hat{y}$は予測された$y$で、$\bar{y}$は$y_{i}$の平均値です。決定係数は、精度がよいほど1に近くなります。0.8以上の数値であれば精度よく予測できていると言えるので今回の例では十分な精度が出ているということができます。
なお、取得は簡単でscoreメソッドに、テスト用のtest_x, test_yを渡すことで$R^{2}$を計算してくれます。
回帰直線の描画
# ===== 線形回帰結果の線を引く
xfit = np.linspace(np.min(x), np.max(x), 1000)
# Y軸はpredictを実行して計算
yfit = model.predict(xfit[:, np.newaxis])
plt.plot(xfit, yfit)
plt.show()上記部分は、未知の値(xfit)に対する予測(yfit)をしているところです。結果については、matplotlibのplotで描画しています。
線形重回帰
線形重回帰とは、1つの予測したいデータ$y$を複数のデータ$x_{i}$から求める回帰分析方法です。式で表すと以下になります。
\[
y = \beta_{0}x_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+…+\epsilon
\]
$(x_{0}, x_{1}, x_{2},…,x_{n})$と$y$のセットの学習データから、係数$\beta_{i}$とバイアス$\epsilon$を推定します。
実装例
線形重回帰は、単回帰と同じようにscikit-learnのLinearRegressionを使用して以下のようなプログラムで実行できます。
import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
def main():
rs = np.random.RandomState(123)
# ===== 線形重回帰を行うためのデータを生成する
bias = 5.0
x, y, coef = make_regression(
n_samples=10000,
n_features=10,
n_informative=3,
n_targets=1,
coef=True,
bias=bias,
noise=5.0,
random_state=rs,
)
np.set_printoptions(precision=3, suppress=True)
print(f"true coef: {coef}")
print(f"true bias: {bias:.3f}")
# 学習用データとテスト用データを分割する
train_x, test_x, train_y, test_y = train_test_split(x, y, random_state=rs)
# ===== 線形重回帰モデルを生成する
model = LinearRegression(fit_intercept=True)
# ===== モデルを学習する
model.fit(train_x, train_y)
# パラメータを表示する
print(f"coef: {model.coef_}")
print(f"bias: {model.intercept_:.3f}")
print(f"R2: {model.score(test_x, test_y):.3f}")
if __name__ == "__main__":
main()【実行結果例】 true coef: [ 0. 0. 0. 0. 64.063 0. 96.22 0. 0. 91.392] true bias: 5.000 coef: [ 0.01 0.065 -0.208 -0.041 64.05 0.082 96.311 -0.03 0.012 91.432] bias: 4.897 R2: 0.999
実装内容の解説
重回帰と言いつつも単回帰と実装方法は同じですので少し異なる部分のみ説明します。
データセットの用意
# ===== 線形重回帰を行うためのデータを生成する
bias = 5.0
x, y, coef = make_regression(
n_samples=10000,
n_features=10,
n_informative=3,
n_targets=1,
coef=True,
bias=bias,
noise=5.0,
random_state=rs,
)データを生成するときにn_featureを10としています。これは$x_{0}$~$x_{9}$までの10の特徴を持つデータを用意していることを意味しています。$y$は一つなので、n_targets=1です。
n_infomativeは、変数のうち$y$を説明するのに寄与している変数の数を指定しています。今回3を指定しているため、10変数あるわけですが、yの変化に影響を与えるのは3変数のみであることを示しています。
true coef: [ 0. 0. 0. 0. 64.063 0. 96.22 0. 0. 91.392]
上記のようにデータ生成時に返却される真値であるcoefを見てもらえば分かりますが、3つの部分しか係数に値を持っていません。数式でいうところの$y = \beta_{0}x_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+…+\epsilon$の中で$\beta$が0ということですので、$x$がどんな値をとろうが、$y$の値は変わりません。
線形回帰モデルの生成と学習
# ===== 線形重回帰モデルを生成する
model = LinearRegression(fit_intercept=True)
# ===== モデルを学習する
model.fit(train_x, train_y)
# パラメータを表示する
print(f"coef: {model.coef_}")
print(f"bias: {model.intercept_:.3f}")
print(f"R2: {model.score(test_x, test_y):.3f}")上記の部分を見てもらえば分かりますが、重回帰であろうがプログラムの方法は変わりません。結果について見てみましょう。
true coef: [ 0. 0. 0. 0. 64.063 0. 96.22 0. 0. 91.392] true bias: 5.000 coef: [ 0.01 0.065 -0.208 -0.041 64.05 0.082 96.311 -0.03 0.012 91.432] bias: 4.897 R2: 0.999
ちゃんと真の係数が0になっているところは0に近い係数が予測できていますし、値を持っているところは近い値を予測できています。また、決定係数も1に近いことから精度よく予測できていることが分かります。
まとめ
scikit-learnのLinearRegressionを使用して線形回帰する方法について紹介してきました。簡単なコードで線形回帰によるデータ予測ができることが理解いただけたかと思います。
このようにデータに対してモデルの当てはめができると例えば、データがどのような傾向でで増加していく(又は減少していく)傾向があるのかなどを簡単に調べることができます。是非、色々なデータに対して線形回帰を試してみていただけたらと思います。
上記で紹介しているソースコードについては GitHub にて公開しています。参考にしていただければと思います。







